Регистрация Спросить otvet5GPT
WallBox
10.05.2022 03:10
Математика
Есть ответ 👍

решить уравнение 2sin^2(2x)=(cosx+sinx)^2

102
383
Посмотреть ответы 2

Ответы на вопрос:

StenxgenS
StenxgenS
4,6(64 оценок)

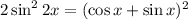
2\sin^{2}2x = (\cos x + \sin x)^{2}

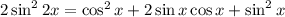
2\sin^{2}2x = \cos^{2}x + 2\sin x \cos x + \sin^{2}x

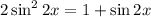
2\sin^{2}2x = 1 + \sin 2x

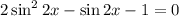
2\sin^{2}2x - \sin 2x - 1 = 0

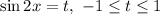
Замена: \sin 2x = t, \ -1 \leq t \leq 1

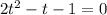
2t^{2} - t - 1 = 0

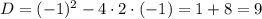
D = (-1)^{2} - 4 \cdot 2 \cdot (-1) = 1 + 8 = 9

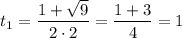
t_{1} = \dfrac{1 + \sqrt{9}}{2 \cdot 2} = \dfrac{1 + 3}{4} = 1

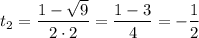
t_{2} = \dfrac{1 - \sqrt{9}}{2 \cdot 2} = \dfrac{1 - 3}{4} = -\dfrac{1}{2}

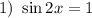
1) \ \sin 2x = 1

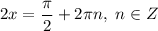
2x = \dfrac{\pi}{2} + 2\pi n, \ n \in Z

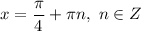
x = \dfrac{\pi}{4} + \pi n, \ n \in Z

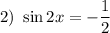
2) \ \sin 2x = -\dfrac{1}{2}

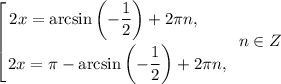
\displaystyle \left [ {{2x =\arcsin \left(-\dfrac{1}{2} \right) + 2\pi n, \ \ \ \ \ } \atop {2x =\pi - \arcsin \left(-\dfrac{1}{2} \right) + 2\pi n, }} \right. \ n \in Z

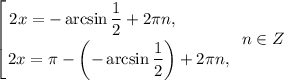
\displaystyle \left [ {{2x =-\arcsin \dfrac{1}{2} + 2\pi n, \ \ \ \ \ \ \ \ \ \, } \atop {2x =\pi - \left(-\arcsin \dfrac{1}{2}\right) + 2\pi n,}} \right. \ n \in Z

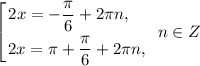
\displaystyle \left [ {{2x =-\dfrac{\pi}{6} + 2\pi n, \ \ \ } \atop {2x =\pi + \dfrac{\pi}{6} + 2\pi n, }} \right. \ n \in Z

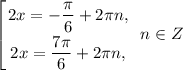
\displaystyle \left [ {{2x =-\dfrac{\pi}{6} + 2\pi n,} \atop {2x = \dfrac{7\pi}{6} + 2\pi n, }} \right. \ n\in Z

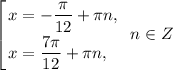
\displaystyle \left [ {{x =-\dfrac{\pi}{12} + \pi n,} \atop {x = \dfrac{7\pi}{12} + \pi n, \ \ }} \right. \ n\in Z

Получили три ответа с наименьшим положительным периодом 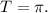T = \pi.

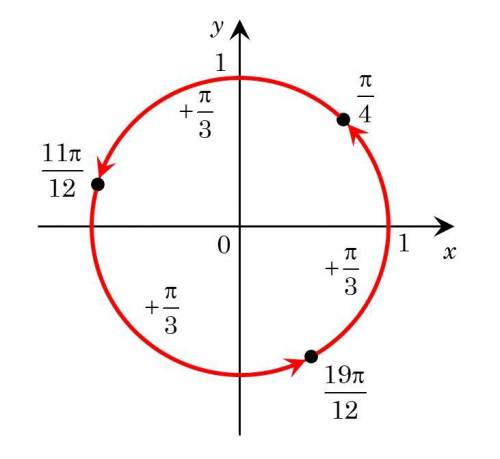
На единичной окружности найдем объединение всех ответов. Заметим, что все три ответа повторяются через треть окружности (см. рисунок), поэтому: 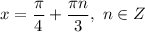x = \dfrac{\pi}{4} + \dfrac{\pi n}{3}, \ n \in Z

ответ: 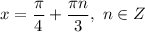x = \dfrac{\pi}{4} + \dfrac{\pi n}{3}, \ n \in Z


решить уравнение 2sin^2(2x)=(cosx+sinx)^2
верника3
верника3
4,6(32 оценок)

p=a+b+c; с= p-(a+b) с=186-126=60мм ответ: 60 мм

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS