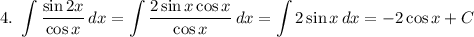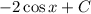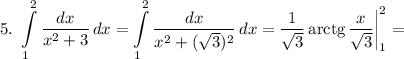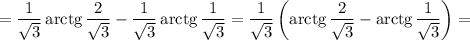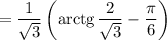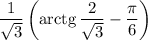Ответы на вопрос:
ответ:
x=+-pi/3+2pi*n n∈z
пошаговое объяснение:
заменим
2sin^2x=2(1-cos^2x)=2-2cos^x
подставим
2-2cos^x+3cosx=0
обозначим
cosx=t
получим
2-2t^2+3t=0
преобразуем:
-2t^2+3t+2=0
решаем:
d=9-4*(-2)*2=9+16=25
t 1/2 =(-3+-5)/(2*2) => t1=-8/4=-2 t2=2/4=1/2
cosx=-2
нет решений
cosx=1/2
x=+-arccos(1/2)+2pi*n
x=+-pi/3+2pi*n n∈z
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Математика
-
Розв язати рівняння 8/9+x=1...
 succura26.09.2022 04:12
succura26.09.2022 04:12 -
|-1/2|:|-2| = мбвхажыд...
 Ксюшалебедева02.09.2022 15:42
Ксюшалебедева02.09.2022 15:42 -
3.Решите системы уравнений: а подстановки сложения...
 vanyavanyaere24.07.2021 16:58
vanyavanyaere24.07.2021 16:58 -
Скоротіть дріб: 32−5х−22−4 с пошаговым объяснением...
 КостянЕрмаков2329.04.2022 10:59
КостянЕрмаков2329.04.2022 10:59 -
3. Маса торта 2 кг 400 г. Яка маса A 24 r; Б 240 г; 1 10 частини...
 Ичиносе18.08.2021 20:30
Ичиносе18.08.2021 20:30 -
Вкажіть координати точки C...
 deaflora12.12.2022 11:59
deaflora12.12.2022 11:59 -
6 : ⅓ - 0,8:1,5/3/2•0,4...
 алина20042303.02.2023 03:24
алина20042303.02.2023 03:24 -
У МЕНЯ ЕСТЬ 10 минут 4. Начертите окружность радиуса 3см. с...
 SadPlayer00728.11.2020 14:57
SadPlayer00728.11.2020 14:57 -
5 На фермі всього 320 тварин. Корови становлять ycieï - 2. Решта...
 FedShar2801.08.2021 18:20
FedShar2801.08.2021 18:20 -
М(-1;-3);N(3;1);K(0;4);P(3;-2) знайти координати точки MN i...
 Anzhelika062421.03.2023 16:41
Anzhelika062421.03.2023 16:41

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

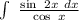 5. Вычислите
5. Вычислите 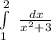 очень заранее огромное
очень заранее огромное