Регистрация Спросить otvet5GPT
Сауле121
11.01.2022 19:32
Геометрия
Есть ответ 👍

Дано A(3:-5:-2), B(-4:2:3), C(-2:-4:5). Найти косинус угла А

187
187
Посмотреть ответы 2

Ответы на вопрос:

elizaveta1705fomina
elizaveta1705fomina
4,7(52 оценок)

ответ: cosA=5√41

Объяснение: если треугольник прямоугольный, то вычислим наибольшую его сторону: АВ; ВС; АС по формуле:

АB²=(Ах-Ау)²+(Ау-Ву)²+(Аz-Bz)²;

AB²=(3-(-4))²+(-5-2)²+(-2-3)²=

=(3+4)²+(-7)²+(-5)²=7²+49+25=49+74=123

AB=√123=3√41

Остальные стороны найдём по этой же формуле:

BC²=(-4-(-2))²+2-(-4))²+(3-5)²=

=(-4+2)²+(2+4)²+(-2)²=(-2)²+6²+4=4+36+4=44

ВС=√44=2√11

АС²=(3-(-2))²+(-5-(-4))²+(-2-5)²=

=(3+2)²+(-5+4)²+(-7)²=5²+(-1)²+49=25+1+49=

=75; АС=√75=5√3

Итак: АВ=√123=3√41; ВС=√44=2√11;

АС=√75=5√3

Самая большая сторона АВ, значит она и является гипотенузой. Гипотенуза лежит напротив угла 90°, значит этим углом является угол С. Косинус-это отношение прилежащего к углу катета к гипотенузе, поэтому cosA=AC/AB=√75/√123=√(75/123)=

=(√25/41)=5/√41


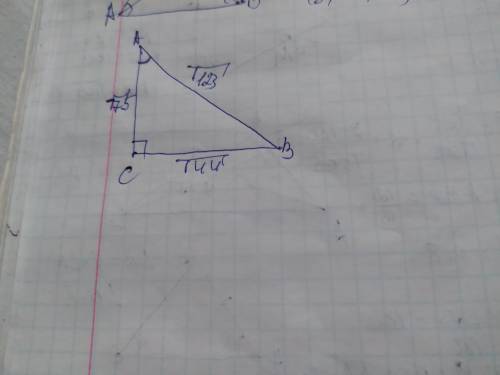
Дано A(3:-5:-2), B(-4:2:3), C(-2:-4:5). Найти косинус угла А
Викуша0402
Викуша0402
4,7(8 оценок)

∆АВС- прямоугольный треугольник

По Теореме Пифагора

АС=√(АВ²+ВС²)=√(3²+4²)=5см

∆АА1С- прямоугольный треугольник

∠А1АС=90°; ∠А1СА=60°; ∠АА1С=30°

АС- катет против угла ∠АА1С=30°

А1С=2*АС=2*5=10см

ответ: 10см


в прямой четырехугольной призме в основании лежит прямоугольник со сторонами 3 и 4 см диагональ приз

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Геометрия

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS