Регистрация Спросить otvet5GPT
kvas1985
22.06.2020 06:34
Алгебра
Есть ответ 👍

Вместо n надо подставить 8

204
266
Посмотреть ответы 2

Ответы на вопрос:

karinka20001202
karinka20001202
4,8(91 оценок)

a)

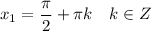
x_1 = \dfrac{\pi}{2} + \pi k ~~~ k\in Z

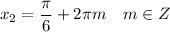
x_2 = \dfrac{\pi}{6} + 2\pi m~~~ m\in Z  

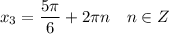
x_3 = \dfrac{5\pi}{6} + 2\pi n~~~ n\in Z

б)

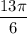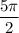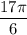 \dfrac{13\pi}6};   \dfrac{5\pi }{2};   \dfrac{17\pi}6};

Объяснение:

a)

sin (8π + 2x) = cos x

sin 2x = cos x

2 sin x · cos x - cos x = 0

cos x (2sin x - 1) = 0

1) cos x = 0

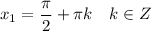
x_1 = \dfrac{\pi}{2} + \pi k ~~~ k\in Z

2) 2sin x - 1 = 0

sin x = 1/2

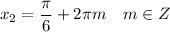
x_2 = \dfrac{\pi}{6} + 2\pi m~~~ m\in Z

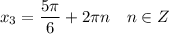
x_3 = \dfrac{5\pi}{6} + 2\pi n~~~ n\in Z

б) х∈ [2π;  3π]

1)

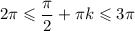
2\pi \leqslant \dfrac{\pi}{2} + \pi k \leqslant 3\pi

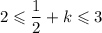
2 \leqslant \dfrac{1}{2} + k \leqslant 3

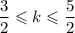
\dfrac{3}{2} \leqslant k \leqslant \dfrac{5}{2}

k = 2

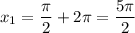
x_1 = \dfrac{\pi}{2} + 2\pi = \dfrac{5\pi }{2}

2)

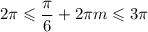
2\pi \leqslant \dfrac{\pi}{6} + 2\pi m \leqslant 3\pi

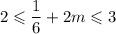
2 \leqslant \dfrac{1}{6} + 2 m \leqslant 3

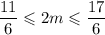
\dfrac{11}{6} \leqslant 2 m \leqslant \dfrac{17}{6}

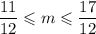
\dfrac{11}{12} \leqslant m \leqslant \dfrac{17}{12}

m = 1

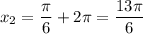
x_2 = \dfrac{\pi}{6} + 2\pi = \dfrac{13\pi}6}

3)

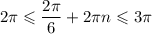
2\pi \leqslant \dfrac{2\pi}{6} + 2\pi n \leqslant 3\pi

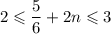
2 \leqslant \dfrac{5}{6} + 2 n \leqslant 3

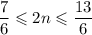
\dfrac{7}{6} \leqslant 2 n\leqslant \dfrac{13}{6}

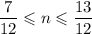
\dfrac{7}{12} \leqslant n \leqslant \dfrac{13}{12}

n = 1

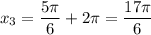
x_3 = \dfrac{5\pi}{6} + 2\pi = \dfrac{17\pi}6}

mrrosslanp0aahw
mrrosslanp0aahw
4,7(81 оценок)
(х - 2 )^2 - ( х + 1 )( х - 3 ) = х^2 - 4х + 4 - ( х^2 - 3х + х - 3 ) = х^2 - 4х + 4 - х^2 + 2х + 3 = - 2х + 7 ответ ( - 2х + 7 )

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS