(в моих вопросах также есть другие нерешенные задания, буду благодарна, если заглянете))

278

415

Посмотреть ответы 2

Ответы на вопрос:

zhahbota

Математика

4,8(28 оценок)

1). Первое число.

Вначале сделаем некоторые упрощения (основные свойства корней и степеней, фактически никаких подсчетов):

$\displaystyle 0,6^{\frac{1}{3} } \cdot 1,3 ^{- \frac{2}{5} } = \sqrt[3]{0,6^1} \cdot \frac{1}{1,3 ^ \frac{2}{5} } = \sqrt[3]{0,6} \cdot \frac{1}{ \sqrt[5]{1,3^2} } = \sqrt[3]{0,6} \cdot \sqrt[5]{\frac{1}{{1,3^2} } } =\\\\= \sqrt[15]{0,6^5} \cdot \sqrt[15]{\frac{1^3}{1,3^6 } } = \sqrt[15]{ \frac{0,6^5}{1,3^6} }$

А теперь можно либо посчитать, что находится под корнем, либо избежать муторных вычислений и сразу сказать, что числитель меньше знаменателя, и дробь меньше единицы. Значит, и корень из такой дроби тоже меньше единицы.

Итог: число 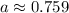$a \approx 0.759$ не подходит.

2). Второе число.

Расписываю менее подробно:

$\displaystyle 0,7^{- \frac{2}{3} } \cdot 0,3^{- \frac{1}{5} } = \sqrt[3]{\frac{1}{0,7^2} } \cdot \sqrt[5]{\frac{1}{0,3^1} } = \sqrt[15]{\frac{1}{0,7^{10}} } \cdot \sqrt[15]{\frac{1}{0,3^3} } = \sqrt[15]{ \frac{1}{0,7^{10} \cdot 0,3^3} }$

Очевидно, что знаменатель в подкоренном выражении меньше единицы, поэтому само подкоренное выражение больше единицы. И корень больше единицы.

Итог: число 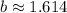$b \approx 1.614$ подходит.

3). Третье число.

И, наконец, последнее число:

$\displaystyle 1,8^{\frac{1}{3} } \cdot 0,3^{-\frac{2}{5} } = \sqrt[3]{1,8} \cdot \sqrt[5]{\frac{1}{0,3^2} } = \sqrt[15]{1,8^5} \cdot \sqrt[15]{\frac{1}{0,3^6} } = \sqrt[15]{ \frac {1,8^5}{0,3^6} }$

Здесь, опять, подкоренное выражение больше единицы (по вполне понятным причинам), так что и сам корень будет больше единицы.

Итог: число 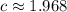$c \approx 1.968$ подходит.

ответ: b и c.

аленка1опр

Математика

4,6(21 оценок)

Ответ №2.

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.