Регистрация Спросить otvet5GPT
katrinzeta18
29.06.2022 10:46
Математика
Есть ответ 👍

Найдите объем тела, заданного ограничивающими его поверхностями

154
487
Посмотреть ответы 2

Ответы на вопрос:

anyta006
anyta006
4,6(56 оценок)

Пошаговое объяснение:

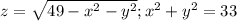
z= \sqrt{49-x^{2}-y^2 } ; x^{2} +y^2 = 33

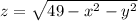z= \sqrt{49-x^{2}-y^2 } - это верхняя половина сферы с радиусом 7 и центром в начале координат

х² + у² = 33 - это цилиндр с осью по OZ радиусом r = √33

рисунок прилагается

найдем пересечение этих фигур

z = √(49-33) = √16 = 4

V = ∫∫∫dx dy dz

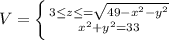
V = \left \{ {{3\leq z\leq =\sqrt{49-x^{2}-y^2 } } \atop {x^2+y^2=33}} \right.

перейдем к цилиндрическим координатам

\left[\begin{array}{ccc}r cos\alpha\\y= r sin\alpha ;dxdydz=rdrd\\ z=z\end{array}\right]

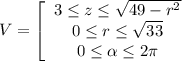
V = \left[\begin{array}{ccc}{3\leq z \leq \sqrt{49-r^2}\\{0\leq r\leq \sqrt{33} \\0\leq \alpha \leq 2\pi \end{array}\\

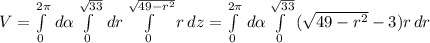
V=\int\limits^{2\pi }_0 {} \, d\alpha \int\limits^{\sqrt{33}} _0 {} \, dr \int\limits^{\sqrt{49-r^2} }_0 {r} \, dz =\int\limits^{2\pi }_0 {} \, d\alpha \int\limits^{\sqrt{33}} _0 {(\sqrt{49-r^2}-3})r \, dr

посчитаем

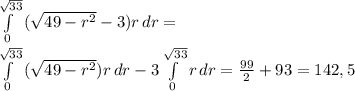
\int\limits^{\sqrt{33}} _0 {(\sqrt{49-r^2}-3})r \, dr =\\ \int\limits^{\sqrt{33}} _0 {(\sqrt{49-r^2}})r \, dr -3\int\limits^{\sqrt{33}} _0 r \, dr =\frac{99}{2}+93 = 142,5

теперь, наконец, посчитаем объем

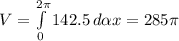
V = \int\limits^{2\pi }_0 {142.5} \, d\alpha x = 285\pi

           

GeCUri
GeCUri
4,7(34 оценок)

Необходимо число поделить на количество процентов, которое оно составляет, и результат умножить на 100.

а)

3/1

* 100 = 300;

б)

40/10

* 100 = 4 * 100 = 400;

в)

30/15

* 100 = 2 * 100 = 200;

г)

250/50

* 100 = 5 * 100 = 500.

а) 300;

б) 400;

в) 200;

г) 500.

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS