Евгеха001

26.12.2021 10:42

Геометрия

Есть ответ 👍

В равнобедренном треугольнике площадью 9√3(девять корень из трёх) см один из углов равен 120°. Найдите боковую сторону.

298

487

Посмотреть ответы 3

Ответы на вопрос:

danilkalmykov1

Геометрия

4,8(26 оценок)

ответ: 6 cm

Объяснение: Площадь равнобедренного треугольника можно вычислить по формуле:

S= a^2*sinA /2, (1) где а-длина боковой стороны, А- угол при вершине треугольника

Заметим, что данный треугольник -тупоугольный, значит угол при вершине 120 град

Тогда (1) можем переписать так:

а^2*sin120/2=9√3

a^2*sin60=18√3

a^2*√3/2=18√3

a^2=36

a=6 cm

007София

Геометрия

4,5(9 оценок)

Дано:

Равнобедренный треугольник.

S = 9√3 см².

Один из углов = 120°.

Найти:

Боковая сторона = ? см.

Решение:

Обозначим равнобедренный треугольник буквами A, B и C.

Пусть ∠B - один из внутренних углов ΔABC, равный 120°.

Формула площади данного треугольника:

S ΔABC = 1/2 * a² * sin(B), где a - боковая сторона.

Т. к. площадь этого треугольника нам известна, приравняем данную формулу к значению площади ΔABC и решим полученное уравнение:

1/2 * a² * sin(B) = 9√3

1/2 * a² * sin(120°) = 9√3

(1/2)a² * (√3)/2 = 9√3

1/2 * ((√3)/2)a² = 9√3

((√3)/4)a² = 9√3

a² = 4 * 9

a² = 36

a = ± √36

a₁ = 6; a₂ = -6

Так как единица измерения не может быть отрицательным числом

⇒ a = 6 см.

В равнобедренном треугольнике боковые стороны равны.

⇒ AB = BC = 6 см.

ответ: 6 см.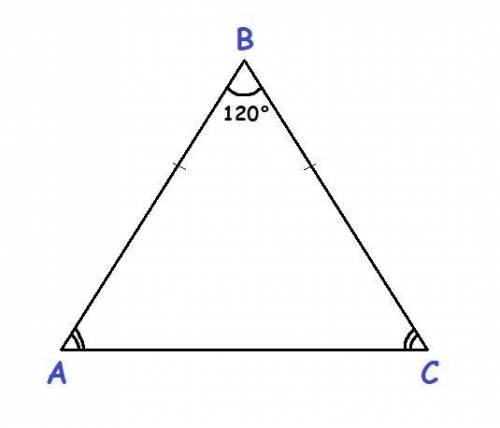
В равнобедренном треугольнике площадью 9√3(девять корень из трёх) см один из углов равен 120°. Найди

диван111111

Геометрия

4,4(65 оценок)

По теореме косинусов мы имеем ab2=ac2+bc2−2.ac.bc.cos∠acbab2=ac2+bc2−2.ac.bc.cos⁡∠acb . подставляя вместо ac , bc и угла их значения, мы получаем: ab2=122+102−2⋅12⋅10⋅cos(60∘)

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.