Регистрация Спросить otvet5GPT
zaijiki
16.01.2020 22:14
Математика
Есть ответ 👍

Числа F0, F1, F2,... заданы так: F0=0, F1=1, Fn+2=Fn+1+Fn для n=0,1,2 Докажите, что для каждого n большего или равного 0 подходит:
Fn меньше/равно ((1+ корень из 5)/2)в степени n-1

272
287
Посмотреть ответы 2

Ответы на вопрос:

JûšțĞîřł
JûšțĞîřł
4,6(21 оценок)

Докажем тождество 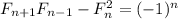F_{n+1}F_{n-1}-F_{n}^2=(-1)^n. Для этого заметим, что \left[\begin{array}{cc}1&1\\1&0&\end{array}\right]^n= \left[\begin{array}{cc}F_{n+1}&F_{n}\\F{n}&F_{n-1}&\end{array}\right], что легко доказывается по индукции. Взяв определитель от обеих сторон, приходим к требуемому.

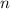
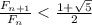Теперь докажем лемму: для любого четного n\frac{F_{n+1}}{F_{n}} < \frac{1+\sqrt{5}}{2}.

Доказательство: пусть 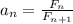a_{n}=\frac{F_{n}}{F_{n+1}}. Сразу примем, что предел этой последовательности существует. Это равносильно 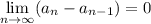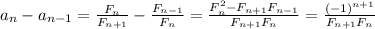\lim\limits_{n\to\infty}(a_{n}-a_{n-1})=0.a_{n}-a_{n-1}=\frac{F_{n}}{F_{n+1}}-\frac{F_{n-1}}{F_{n}}=\frac{F_{n}^2-F_{n+1}F_{n-1}}{F_{n+1}F_{n}}=\frac{(-1)^{n+1}}{F_{n+1}F_{n}}. Отсюда очевидно, что 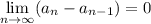\lim\limits_{n\to\infty}(a_{n}-a_{n-1})=0. Пусть 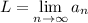L=\lim\limits_{n\to\infty}a_{n}. Тогда 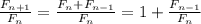\frac{F_{n+1}}{F_{n}}=\frac{F_{n}+F_{n-1}}{F_{n}}=1+\frac{F_{n-1}}{F_{n}}. Взяв предел от обеих частей, приходим к 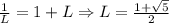\frac{1}{L}=1+L \Rightarrow L=\frac{1+\sqrt{5}}{2}.  Поскольку 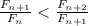\frac{F_{n+1}}{F_{n}}<\frac{F_{n+2}}{F_{n+1}} (применяя тождество, получаем разницу 1), лемма доказана.

Теперь по индукции.

База 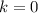k=0 очевидна. Пусть для всех 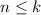n\leq k это верно. Докажем, что 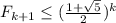F_{k+1}\leq (\frac{1+\sqrt{5}}{2})^k . Пусть 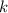k четно, тогда 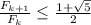\frac{F_{k+1}}{F_{k}}\leq \frac{1+\sqrt{5}}{2}, домножая на 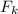F_{k} и применяя предположение индукции, получаем требуемое. Теперь неравенство выполняется для всех 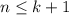n\leq k+1. Далее берем 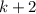k+2 — четное число — и повторяем операцию. Тем самым докажем для всех нечетных чисел.

Теперь докажем для всех четных. 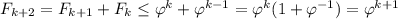F_{k+2}=F_{k+1}+F_{k}\leq \varphi^k+\varphi^{k-1}=\varphi^k(1+\varphi^{-1})=\varphi^{k+1}, что и требовалось

PolinaZinoviva
PolinaZinoviva
4,4(52 оценок)
Ответ уравнения 2548.

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS