Регистрация Спросить otvet5GPT
seraoki557
30.06.2021 07:18
Математика
Есть ответ 👍

Найти площадь фигуры, ограниченной линиями y=-x^2+2, y=x.

273
284
Посмотреть ответы 2

Ответы на вопрос:

CTpeJIa333
CTpeJIa333
4,7(72 оценок)
Решение:

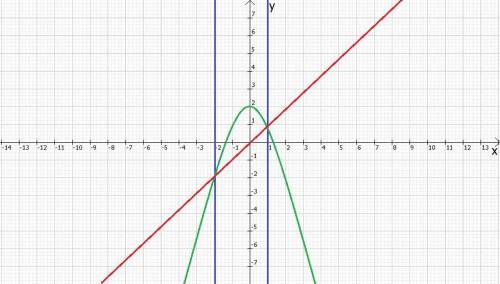
Найдём абсциссы точек пересечения графиков функций. Для этого необходимо приравнять данные функции и решить уравнение:

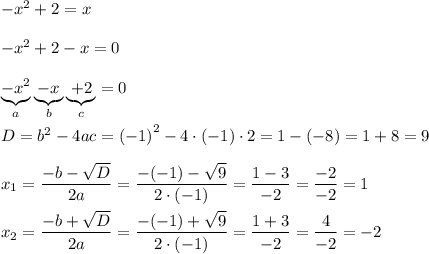
{-x}^{2}+2=x \\ \\ {-x}^{2}+2-x=0 \\ \\ \underbrace{{-x}^{2}}_{a}\underbrace{-x}_{b}\underbrace{+2}_{c}=0 \\ \\ D={b}^{2}-4ac={(-1)}^{2}-4\cdot(-1)\cdot2=1-(-8)=1+8=9\\\\{x}_{1}=\dfrac{-b-\sqrt{D}}{2a}=\dfrac{-(-1)-\sqrt{9}}{2\cdot(-1)}=\dfrac{1-3}{-2}=\dfrac{-2}{-2}=1 \\ \\ {x}_{2}=\dfrac{-b+\sqrt{D}}{2a}=\dfrac{-(-1)+\sqrt{9}}{2\cdot(-1)}=\dfrac{1+3}{-2}=\dfrac{4}{-2}=-2

Теперь воспользуемся формулой Ньютона-Лейбница:

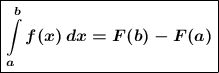
\boxed{\boldsymbol{\int\limits^b_a {f(x)} \, dx =F(b)-F(a)}}

Где 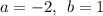a=-2, \: \: b=1. Нам ничего не остаётся сделать, как подставить численные значения в формулу и решить определённый интеграл:

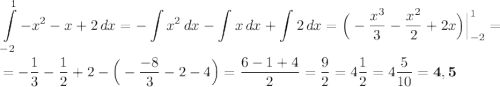
\displaystyle \int\limits^1_{-2} {{-x}^{2}-x+2} \, dx =-\int\limits {{x}^{2}} \, dx -\int\limits {x} \, dx +\int\limits {2} \, dx =\Big(-\dfrac{{x}^{3}}{3}-\dfrac{{x}^{2}}{2}+2x\Big)\Big|^1_{-2}= \\ \\ =-\dfrac{1}{3}-\dfrac{1}{2}+2-\Big(-\dfrac{-8}{3}-2-4\Big)=\dfrac{6-1+4}{2}=\dfrac{9}{2}=4\dfrac{1}{2}=4\dfrac{5}{10}=\bf{4,5}

ответ: \Large{\boxed{\bold{4,5}}}
Найти площадь фигуры, ограниченной линиями y=-x^2+2, y=x.
Deni11111111
Deni11111111
4,6(60 оценок)
902/55=16 =16.4

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS