Ответы на вопрос:
X² -x-2 > 0 парабола, ветви направлены вверх х²-х-2=0 д=1+4*2=9 х₁= 1-3 = -1 2 х₂= 1+3 =2 2 + + -1 2 \\\\\\\\\\ - \\\\\\\\\ х∈(-∞; -1)∨(2; +∞)
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
В каком случае даны прямо пропорциональные величины...
 vaxa1234523.06.2022 15:29
vaxa1234523.06.2022 15:29 -
Докажи: если y=10/x, то y′=−10/x^2. Опиши шаги доказательства Далее...
 anastasiasestak29.04.2020 06:51
anastasiasestak29.04.2020 06:51 -
Найти полный дефференциал функции...
 IdzSen11.06.2022 10:32
IdzSen11.06.2022 10:32 -
Найти интервалы выпуклости, вогнутости, точки перегиба графиков...
 molkes20.08.2021 21:41
molkes20.08.2021 21:41 -
1. Нарисуйте граф, вершинами которого являются натуральные числа...
 egorshlyahov12p0dhm929.10.2022 18:27
egorshlyahov12p0dhm929.10.2022 18:27 -
быстро решить с объяснением...
 АшадЕфремова29.08.2021 06:25
АшадЕфремова29.08.2021 06:25 -
РЕШИТЬ ПАЖЕ 57.938-2.5x=41.863...
 Алина111657718.03.2022 18:38
Алина111657718.03.2022 18:38 -
Решить неравенство -х^2-2х-6≥0...
 kkarinanexK19.07.2021 05:10
kkarinanexK19.07.2021 05:10 -
Найти наименьший положительный период функции y= 2cos(2x-)...
 никто27131.12.2022 09:55
никто27131.12.2022 09:55 -
В среднем из 100 электролампочек, имеющихся в магазине, одна бывает...
 амина65303.01.2021 02:59
амина65303.01.2021 02:59

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

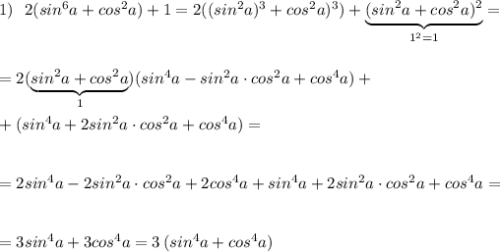
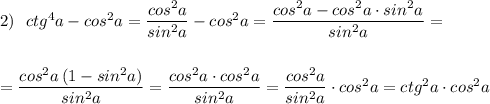

![=\dfrac{cos^2a+2sina\cdot cosa+sin^2a-cos^2a+2sina\cdot cosa-cos^2a}{cos^2a-sin^a}=\\\\\\=\dfrac{4sina\cdot cosa}{cos^2a-sin^2a}=\Big[\ \dfrac{:cos^2a}{:cos^2a}\ \Big]=\dfrac{4\cdot \frac{sina}{cosa}}{1-\frac{sin^2a}{cos^2a}}=\dfrac{4tga}{1-tg^2a}](/tpl/images/3777/9913/97e41.png)