Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
Реши неравенство и запиши ответ в виде числового интервала:...
 умник123567801.06.2023 17:27
умник123567801.06.2023 17:27 -
Відома що 2 с 4. оцініть зеачегня виразу. б) -2,5c+1. ...
 marinka10k01.05.2023 09:54
marinka10k01.05.2023 09:54 -
1.11. 4^4:1000-0,3 8^2•3^3-728 заранее...
 11SOS1110.09.2021 15:24
11SOS1110.09.2021 15:24 -
4 первых вопроса - Найдите общий знаменатель...
 Laly00922.01.2020 08:46
Laly00922.01.2020 08:46 -
Спростіть дріб 14х2у6 : 35х4у...
 мурадаббасов02.07.2020 14:59
мурадаббасов02.07.2020 14:59 -
Решите систему равнение любым кроме графического...
 roshko200209.08.2021 07:40
roshko200209.08.2021 07:40 -
Точка принадлежит отрезку KO, длина которого рав- на 28 см. Найдите длины отрезков...
 lilija64716.10.2020 06:37
lilija64716.10.2020 06:37 -
Нужна по за 8 класс : известно, что 4a+8b=10. найдите значение выражения: 2)...
 muy504.04.2021 18:05
muy504.04.2021 18:05 -
−1,76x+93xy2+21xy2 если x=5 и y=0,2 ....
 аня293302.02.2021 00:03
аня293302.02.2021 00:03 -
Решитe уравнение методом неопределенных коэффициентов:...
 evika844406.02.2021 06:55
evika844406.02.2021 06:55

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

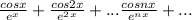
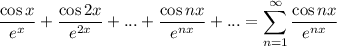
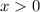
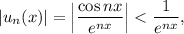 а при
а при 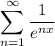 сходится по радикальному признаку Коши:
сходится по радикальному признаку Коши:![\sqrt[n]{\dfrac{1}{e^{nx}} } = \dfrac{1}{e^{x}} < 1,](/tpl/images/3777/9617/beb12.png)
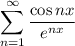 сходится по признаку сравнения при
сходится по признаку сравнения при