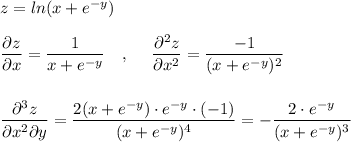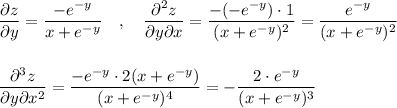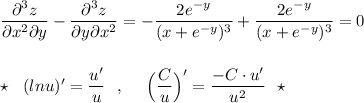Регистрация Спросить otvet5GPT
alina06alina
11.03.2022 01:03
Алгебра
Есть ответ 👍

Проверить, удовлетворяет ли указанному уравнению с частными производными данная функция.

270
467
Посмотреть ответы 3

Ответы на вопрос:

mishka1330
mishka1330
4,5(64 оценок)

z=ln(x+e^{-y})\\\\\dfrac{\partial z}{\partial x}=\dfrac{1}{x+e^{-y}}\ \ \ ,\ \ \ \ \dfrac{\partial ^2z}{\partial x^2}=\dfrac{-1}{(x+e^{-y})^2}\\\\\\\dfrac{\partial ^3z}{\partial x^2\partial y}=\dfrac{2(x+e^{-y})\cdot e^{-y}\cdot (-1)}{(x+e^{-y})^4}=-\dfrac{2\cdot e^{-y}}{(x+e^{-y})^3}

\dfrac{\partial z}{\partial y}=\dfrac{-e^{-y}}{x+e^{-y}}\ \ \ ,\ \ \ \dfrac{\partial ^2z}{\partial y\partial x}=\dfrac{-(-e^{-y})\cdot 1}{(x+e^{-y})^2}=\dfrac{e^{-y}}{(x+e^{-y})^2}\\\\\\\dfrac{\partial ^3z}{\partial y\partial x^2}=\dfrac{-e^{-y}\cdot 2(x+e^{-y})}{(x+e^{-y})^4}=-\dfrac{2\cdot e^{-y}}{(x+e^{-y})^3}

\dfrac{\partial ^3z}{\partial x^2\partial y}-\dfrac{\partial ^3z}{\partial y\partial x^2}=-\dfrac{2e^{-y}}{(x+e^{-y})^3}+\dfrac{2e^{-y}}{(x+e^{-y})^3}=0\\\\\\\star \ \ (lnu)'=\dfrac{u'}{u}\ \ ,\ \ \ \ \Big(\dfrac{C}{u}\Big)'=\dfrac{-C\cdot u'}{u^2}\ \ \star

manshev2018
manshev2018
4,7(32 оценок)

z=ln(x+e^(-y))

dz/dx=1/(x+e^(-y))*(x+e^(-y))'=1/(x+e^(-y))

d2z/dx2=((x+e^(-y))^(-1))'=-(x+e^(-y))^(-2)*(x+e^(-y))'=-1/(x+e^(-y))^2

d3z/dx2dy=(-(x+e^(-y))^(-2))'=-(-2(x+e^(-y)))^(-3)*(x+e^(-y))'=2(x+e^(-y))^(-3)*(-e^(-y))=-2e^(-y)/(x+e^(-y))^3

dz/dy=1/(x+e^(-y))*(x+e^(-y))'=1/(x+e^(-y))*(-e^(-y))=-e^(-y)/(x+e^(-y))

d2z/dydx=(-e^(-y)*(x+e^(-y))^(-1))'=-e^(-y)*((x+e^(-y))^(-1))'=

-e^(-y)*(-((x+e^(-y))^(-2)))*(x+e^(-y))'=e^(-y)/(x+e^(-y))^2

d3z/dydx2=(e^(-y)/(x+e^(-y))^2)'=e^(-y)((x+e^(-y))^(-2))'=

e^(-y)*(-2((x+e^(-y))^(-3)))*(x+e^(-y))'=-2e^(-y)/(x+e^(-y))^3

и все

-2e^(-y)/(x+e^(-y))^3-(-2e^(-y)/(x+e^(-y))^3)=-2e^(-y)/(x+e^(-y))^3+2e^(-y)/(x+e^(-y))^3=0

Объяснение:

Кристина7836
Кристина7836
4,4(69 оценок)

Объяснение:

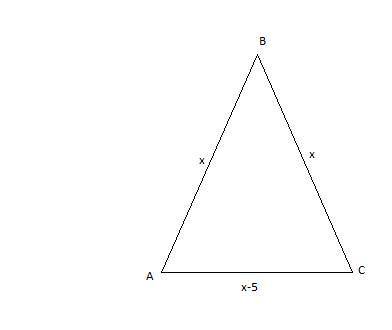
P=31m

x+x+x-5=31

3x-5=31

3x=36

x=12m  

основа a=x-5=12-5=7m

OTBET:основа трикутника дорівнює 7m


Периметр рівнобедреного трикутника дорівнює 31 м. Чому дорівнює основа, якщо вона на 5 м менша від б

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS