Ответы на вопрос:
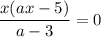
Если 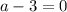 , то есть
, то есть 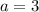 , то уравнение не имеет смысла.
, то уравнение не имеет смысла.
Если 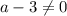 , то есть
, то есть 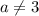 , то:
, то:
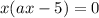
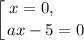
Решим второе уравнение. Имеем: 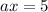
1) Если 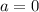 , то имеем уравнение
, то имеем уравнение 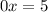 , которое не имеет решений.
, которое не имеет решений.
Имеем один корней: 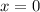
2) Если 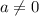 , то
, то 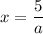
ответ: если 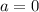 , то
, то 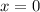 ; если
; если 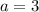 , то нет корней; если
, то нет корней; если 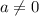 и
и 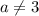 , то
, то 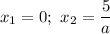
если я правильно понимаю, то неравенство такое
числитель разложил по формуле разности квадратов
чтобы знаменатель разложить, надо решить квадратное уравнение
решаем неравенство методом интервалов.
нули функции
мы уже нашли, когда раскладывали.
осталось только расположить их на числовой оси и расставить знаки
больше всех, это очевидно. далее по убыванию
, затем
, а самое маленькое из них
.
так как дробь была разложена так, что при х во всех скобках коэффициент 1, то в самом правом промежутке "+", а дальше знаки будут чередоватся, так как нет нулей четности кратности (здесь везде степень при скобках равна 1).
промежутки слева направо будут + - + - +
будут включаться, так как неравенство нестрогое и эти значения с числителя, а со знаменателя значения всегда будут "выколотыми".
это и есть наш ответ
ответ:
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
Решите по теореме виета: х’2+3х+2=0...
 sagal6315.04.2023 17:30
sagal6315.04.2023 17:30 -
Реди данных уравнений выберите те, которые имеют тот же корень, что и уравнение...
 artgensh24.03.2021 22:17
artgensh24.03.2021 22:17 -
Решите уравнения: 1) 6,89 + 5,37 + 3,11 + 4,63 2) 36 * 2,7 * 5/8 3)0,3 * 0,783...
 Markizka2210.02.2023 21:56
Markizka2210.02.2023 21:56 -
Х-7=5+а 1- найти х . если а равен больше равно -5 но меньше больше 3 2- найти а...
 splaylive28.03.2020 11:17
splaylive28.03.2020 11:17 -
Вычислить площадь криволинейной трапеции, ограниченной функциями y=1+sin(x) y=0...
 druy07114.07.2021 03:09
druy07114.07.2021 03:09 -
Решите неравенство.x^2-12x -5x+9-x^2...
 evseeva09060106.09.2020 22:55
evseeva09060106.09.2020 22:55 -
Что больше 5 или -8 что больше 4 или -1,5 что больше -6 или 3...
 AngelDarkness12317.05.2023 03:14
AngelDarkness12317.05.2023 03:14 -
При каких значениях p значения двучлена 11p+6 меньше значений двучлена 3p−9 ?...
 tim2005310.03.2023 20:54
tim2005310.03.2023 20:54 -
1.86: егер а³=к болса,а¹²-ін табындар...
 rmshturkop01n7325.08.2021 09:04
rmshturkop01n7325.08.2021 09:04 -
Составте лёгкую на проценты на военную тематику...
 AleksandraZul29.11.2022 20:25
AleksandraZul29.11.2022 20:25

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

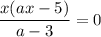 в зависимости от значений параметра
в зависимости от значений параметра 