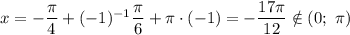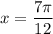Ответы на вопрос:
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
Решите систему уравнений xy-3y-4x=-10 y-2x=-2...
 csgodanilgo07.10.2021 02:48
csgodanilgo07.10.2021 02:48 -
Y=x^2-5x-6 исследуйте функцию и постройте ее график...
 Slvblgo03.12.2022 07:01
Slvblgo03.12.2022 07:01 -
1).решите неравенство: в корне10-х 4-x c системы. 2).найдите площадь...
 ангилино31.07.2022 16:43
ангилино31.07.2022 16:43 -
Розв язати систему рівнянь x+y=2 x-y=0...
 fiskevich214.03.2023 11:58
fiskevich214.03.2023 11:58 -
Представьте выражение в виде рациональной дроби : (х в минус 1...
 lara237714.04.2021 13:27
lara237714.04.2021 13:27 -
Представьте произведение в стандартном виде числа : (3,5*10 в...
 Danielufa15.02.2023 22:36
Danielufa15.02.2023 22:36 -
Решите систему уравнений 1. (в фиг скобке) x-y=3, 2x+3y=16 2.(в...
 11martandreyp0bwg221.07.2020 05:54
11martandreyp0bwg221.07.2020 05:54 -
За 5 кг огурцов и 4 кг помидоров заплатили 220 рублей. сколько...
 Danay290816.05.2020 12:13
Danay290816.05.2020 12:13 -
Розв язати систему рівнянь x+y=3 x-y=1...
 хорёк0504.09.2020 17:35
хорёк0504.09.2020 17:35 -
1/4 * (4х+8) - 2*(1-х) раскройте скобки и подобные слагаемые /...
 loopootoonoo04.02.2021 16:54
loopootoonoo04.02.2021 16:54

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

![cosx + sinx = \frac{1}{\sqrt[2]{2}}](/tpl/images/3776/8367/c30de.png) на интервале x от 0 до pi
на интервале x от 0 до pi 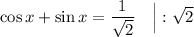
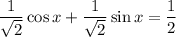
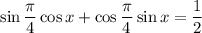
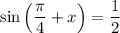
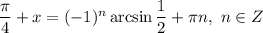
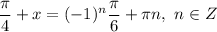
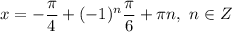
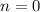 , то
, то 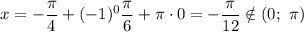
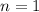 , то
, то 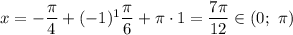
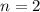 , то
, то 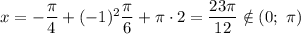
 , то
, то