Регистрация Спросить otvet5GPT
Анастасия0411
03.08.2021 14:53
Математика
Есть ответ 👍

Исследовать на сходимость ряд

220
262
Посмотреть ответы 3

Ответы на вопрос:

Radled
Radled
4,6(15 оценок)

\lim\limits_{n\to\infty}\sqrt[n]{arcsin^n \dfrac{lnn}{n}}=\lim\limits_{n\to\infty}{arcsin \dfrac{lnn}{n}}=(*)

Арксинус непрерывен на всей области определения. Тогда:

(*)={arcsin \lim\limits_{n\to\infty}\dfrac{lnn}{n}}=(**)\\ \lim\limits_{n\to\infty}\dfrac{lnn}{n}=\left[\dfrac{\infty}{\infty}\right]=\lim\limits_{n\to\infty}\dfrac{\frac{1}{n}}{1}=\lim\limits_{n\to\infty}\dfrac{1}{n}=0\\ (**)=arcsin0=0

Тогда, по признаку Коши, ряд сходится

cheburejp00xj4
cheburejp00xj4
4,5(70 оценок)

ряд сходится

Пошаговое объяснение:

используем радикальный признак Коши:

\lim\limits_{n \to \infty} \sqrt[n]{a_n}}= \lim\limits_{n \to \infty} \sqrt[n]{\arcsin^n\frac{\ln n}{n} }}=\lim\limits_{n \to \infty}\arcsin\frac{\ln n}{n} }=\\ \\ =\arcsin \left(\lim\limits_{n \to \infty}\frac{\ln n}{n} }\right)=\arcsin \{ \frac{\infty}{\infty} \}=\arcsin \left(\lim\limits_{n \to \infty}\frac{(\ln n)'}{n'} }\right)= \\ \\ =\arcsin \left(\lim\limits_{n \to \infty}\frac{\frac{1}{n} }{1} }\right)=\arcsin \left(\lim\limits_{n \to \infty}\frac{1}{n} }\right)=

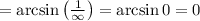
=\arcsin \left(\frac{1}{\infty} }\right)=\arcsin 0=0

0<1, значит ряд сходится

Lasnochas
Lasnochas
4,6(11 оценок)
Т.к. од - биссектриса  ∠вос, то делит его пополам, т.е.∠вод=∠дос=29°∠аод смежен с  ∠дос и вместе составляют развернутый  ∠аос     ⇒  ∠аод=∠аос-∠дос = 180-29=151°

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS