Алгебра: Найти площадь фигуры, ограниченную линиями y=-x^3, y=-x

abdulaevamesed

14.03.2021 19:08

Алгебра

Есть ответ 👍

Найти площадь фигуры, ограниченную линиями y=-x^3, y=-x

256

461

Посмотреть ответы 2

Ответы на вопрос:

Lena747456

Алгебра

4,5(16 оценок)

Решение:

Большое количество задач такого типа решаются при формулы Ньютона-Лейбница:

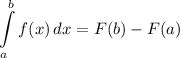
$\displaystyle \int\limits^b_a {f(x)} \, dx = F(b) - F(a)$

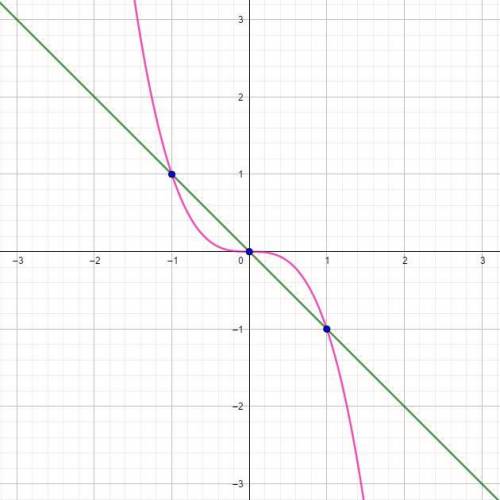
Поэтому, во-первых, нужно найти и 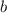- абсциссы точек пересечения графиков функций. Для этого нужно решить несложное уравнение:

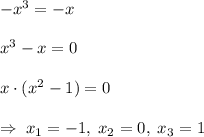
$-x^3 = -x\\\\x^3-x=0\\\\x \cdot (x^2-1)=0\\\\\Rightarrow \; x_1 = -1, \; x_2 = 0, \; x_3 = 1$

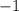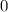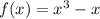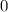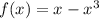А так как есть целых три точки пересечения, то придется считать два интеграла: первый - от до (как результат приравнивания функций: f(x) = x^3-x ), а второй - от до (здесь уже f(x)=x-x^3 ):

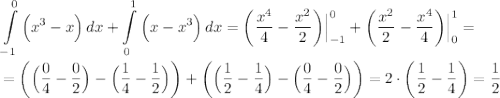
$\displaystyle \int\limits^0_{-1} {\Big (x^3-x \Big) } \, dx + \int\limits^1_{0} {\Big (x-x^3 \Big) } \, dx = \bigg ( \frac{x^4}{4} - \frac{x^2}{2} \bigg ) \Big | ^0_{-1} + \bigg ( \frac{x^2}{2} - \frac{x^4}{4} \bigg ) \Big | ^1_{0} =\\\\= \bigg ( \Big (\frac{0}{4} - \frac{0}{2} \Big ) - \Big (\frac{1}{4} - \frac{1}{2} \Big ) \bigg ) + \bigg ( \Big (\frac{1}{2} - \frac{1}{4} \Big) - \Big (\frac{0}{4} - \frac{0}{2} \Big ) \bigg ) = 2 \cdot \bigg (\frac{1}{2} - \frac{1}{4} \bigg ) = \frac{1}{2}$

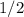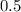Значит, площадь искомой фигуры (состоящей из нескольких других фигур) равна 1/2 или 0.5 (каких-то квадратных единиц измерения), если перевести в десятичную дробь.

ответ: 0.5 .
Найти площадь фигуры, ограниченную линиями y=-x^3, y=-x

Mrfest

Алгебра

4,6(39 оценок)

X²-9=(x-3)(x+3)

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.