В правильной треугольной пирамиде высота равна 3√2 и образует с боковым ребром угол 30 градусов. Найдите объем пирамиды.

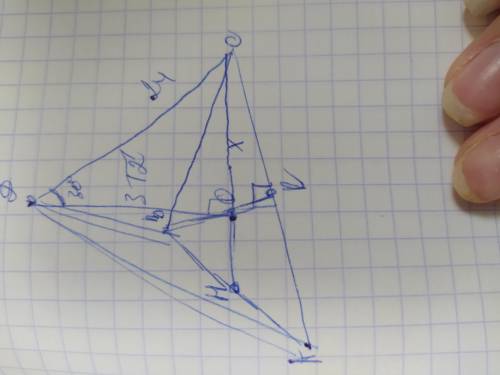
Объяснение: обозначим вершины пирамиды АВСД, а её высоту ДО. Соединим точку О с вершиной С. Получился прямоугольный треугольник ДОС. Угол СДО=30°, а катет СО, лежащий напротив него равен половине гипотенузы ДС. Пусть ОС=х, тогда ДС=2х. Зная величину высоты составим уравнение используя теорему Пифагора:

(2х)²-х²=(3√2)²

4х²-х²=9×2

3х²=18

х²=18/3

х²=6

х=√6

Итак: СО=√6

Проведём медиану- СН и ВК. Они при пересечении в точке О делятся в отношении 2: 1, начиная от вершины угла, и если СО=√6, то ОН=√6/2.

ВК=СН=√6+√6/21,5√6. В правильной трёхугольной пирамиде в основании лежит равносторонний треугольник поэтому медианы СН и ВК являются также его высотами и биссектрисами, делят угол 60° пополам, поскольку в равностороннем треугольнике все углы составляют по 60°. Рассмотрим ∆АВК. Он прямоугольный и АК и ВК являются катетами а АВ- гипотенуза.

Угол АВК=60/2=30°, а катет АК лежащий напротив него равен половине гипотенузы. Пусть АК=у, тогда АВ=2у, зная высоту ВК составим уравнение используя теорему Пифагора:

АВ²-АК²=ВК²

(2у)²-у²=(1,5√6)²

4у²-у²=2,25×6

3у²=13,5

у²=13,5/3

у²=4,5

у=√4,5=3√0,5,

Тогда АВ=ВС=АС=2×3√0,5=6√0,5

Найдём площадь основания по формуле:

S=a²√3/4=(6√0,5)²√3/4=36×0,5√3/4=

=18√3/4=4,5√3(ед²)

Теперь найдём объем пирамиды по формуле: V=⅓×Sосн×ДО=

=⅓×4,5√3×3√2=4,5√3×√2=4,5√6(ед³)

объяснение:

потому как равновеликие фигуры это фигуры с одиннаковой площадью. если четырехуольники равны, то они равновеликие