Математика: Исследовать на сходимость ряд

pstrebykina

10.04.2021 08:10

Математика

Есть ответ 👍

Исследовать на сходимость ряд

206

253

Посмотреть ответы 2

Ответы на вопрос:

filinenok98

Математика

4,6(60 оценок)

Абсолютно сходится

Пошаговое объяснение:

Исследуем на сходимость ряд, состоящий из модулей слагаемых исходного ряда: 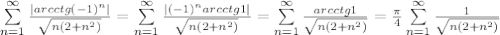$\sum\limits^{\infty}_{n=1} \frac{|arcctg(-1)^n|}{\sqrt{n(2+n^2)}} = \sum\limits^{\infty}_{n=1} \frac{|(-1)^n arcctg1|}{\sqrt{n(2+n^2)}} = \sum\limits^{\infty}_{n=1} \frac{arcctg1}{\sqrt{n(2+n^2)}} = \frac{\pi}{4}\sum\limits^{\infty}_{n=1} \frac{1}{\sqrt{n(2+n^2)}}$

Будем использовать признак сравнения, а именно будем сравнивать этот ряд (с точностью до множителя перед знаком суммы) с 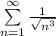$\sum\limits^{\infty}_{n=1}\frac{1}{\sqrt{n^3}}$

Посчитаем предел отношения членов этих рядов:

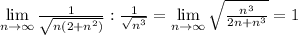
$\lim\limits_{n\rightarrow\infty} \frac{1}{\sqrt{n(2+n^2)}} : \frac{1}{\sqrt{n^3}} = \lim\limits_{n\rightarrow\infty} \sqrt{\frac{n^3}{2n+n^3}}=1$

Этот предел конечный и не равен 0, значит, ряды сходятся или расходятся одновременно. Так как второй ряд имеет вид 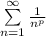$\sum\limits^{\infty}_{n=1} \frac{1}{n^{p}}$ , где p>1, то он сходится, а значит сходится и исходный ряд, причем абсолютно.

trafimozza

Математика

4,6(98 оценок)

Пошаговое объяснение:

49х(2ст.)+28х-28х-16=49х (2степінь)-16

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.