Алгебра: Найдите промежутки убывания функции, если f(х) = х3 + х2-5х+3

svetlanaivanova3

02.03.2023 03:33

Алгебра

Есть ответ 👍

Найдите промежутки убывания функции, если f(х) = х3 + х2-5х+3

128

397

Посмотреть ответы 3

Ответы на вопрос:

lotop

Алгебра

4,6(52 оценок)

Решение:

Сначала найдем производную функции:

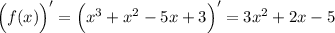
$\Big (f(x) \Big )' = \Big (x^3+x^2-5x+3 \Big )' = 3x^2 + 2x - 5$

Теперь - критические точки производной (то есть те, в которых производная не существует, - таких нет, - и те, в которых она обнуляется, - точки экстремума):

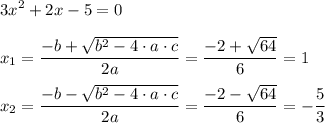
$\displaystyle 3x^2 + 2x-5 = 0\\\\x_1 = \frac{-b+\sqrt{b^2 - 4 \cdot a \cdot c}}{2a} =\frac{-2+\sqrt{64}}{6} = 1 \\\\x_2 = \frac{-b-\sqrt{b^2 - 4 \cdot a \cdot c}}{2a} =\frac{-2-\sqrt{64}}{6} = - \frac{5}{3}$

Осталось только расставить знаки производной:

/////////////////////

+ + + + + + + $\bigg [ \; - \dfrac{5}{3} \; \bigg ]$ - - - - - - - - - $\bigg [\; 1 \; \bigg ]$ + + + + + + + + + +

Функция убывает, если ее производная в данной точке отрицательна. Поэтому искомый промежуток:

${\bigg [ \; - \dfrac{5}{3} ; \; 1 \; \bigg ]}$

Задача решена!

ответ: $\bold {{\bigg [ \; - \dfrac{5}{3} ; \; 1 \; \bigg ]}}$

настя123456789108

Алгебра

4,7(15 оценок)

x∈(-5/3 ; 1) промежуток убывания функции f(х) = х³ + х²-5х+3

Объяснение:

f(х) = х3 + х2-5х+3

f'(x)=3x²+2x-5

f'(x)=3x²+2x-5=0

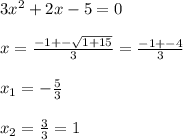
$3x^2+2x-5=0\\\\x=\frac{-1+-\sqrt{1+15} }{3} =\frac{-1+-4}{3} \\\\x_1=-\frac{5}{3} \\\\x_2=\frac{3}{3} =1\\\\$

f'(x)=3x²+2x-5<0

x∈(-5/3 ; 1) промежуток убывания функции f(х) = х³ + х²-5х+3

алалала4

Алгебра

4,6(81 оценок)

Уильяму Шекспиру было 52 года.

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.