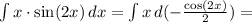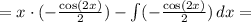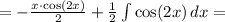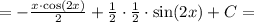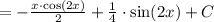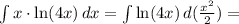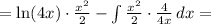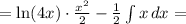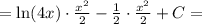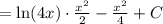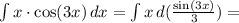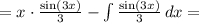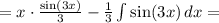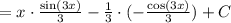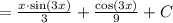Ответы на вопрос:
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Математика
-
Составьте уравнение касательной к графику функции y=x^2+4x+3 в точке...
 nadyushasemeni05.08.2021 23:09
nadyushasemeni05.08.2021 23:09 -
матика............ .....
 ника276212.03.2022 01:00
ника276212.03.2022 01:00 -
сколько будет 1111111+55555555=...
 Кира361116.01.2023 09:16
Кира361116.01.2023 09:16 -
2 фигуры, по одному как сделать? Подскажите...
 Myrasami22.04.2020 14:32
Myrasami22.04.2020 14:32 -
ТОЛЬКО ПОБЫСТРЕЕ,САМОСТОЯТЕЛЬНАЯ ПО МАТЕМАТИКЕ...
 plidap00rk726.03.2022 18:22
plidap00rk726.03.2022 18:22 -
Когда турист три четверти намеченного пути, ему осталось проехать...
 POOTISBIRD5025.09.2020 14:07
POOTISBIRD5025.09.2020 14:07 -
ради мамы Найдите число, если 7/13 от него есть 7/11 от числа 693...
 Nikita2000000513.06.2021 15:29
Nikita2000000513.06.2021 15:29 -
Урок 160 задание номер шесть Какие выражения лица лагман если он...
 Sofa841231.03.2022 09:09
Sofa841231.03.2022 09:09 -
решить задачу в магазин привезли 60кг конфет. в первый день продали...
 мистертомат26.04.2020 11:47
мистертомат26.04.2020 11:47 -
Составьте формулу для вычисления площади фигуры a b c...
 nadyalewoxtphe02.03.2023 22:30
nadyalewoxtphe02.03.2023 22:30

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.