Регистрация Спросить otvet5GPT
виталька1001
06.06.2021 03:24
Алгебра
Есть ответ 👍

7. Радиус основания конуса равен 5 см, а образующая конуса равна 13 см. Найдите объём конуса, и площадь полной поверхности.

221
498
Посмотреть ответы 3

Ответы на вопрос:

цыпабезума
цыпабезума
4,7(47 оценок)

Відповідь:

Объём конуса: 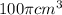100 \pi cm^{3} , Площадь полн. поверхности: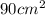 90 cm^{2}

Пояснення:

Площадь полной поверхности конуса можно вычислить по формуле: 

S= S1 +S2,

где S1 - площадь осн., S2 - площадь бок. поверхности.

Площадь осн. конуса: 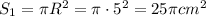 S_1= \pi R^2= \pi \cdot 5^2=25 \pi cm^{2}

Площадь бок. поверхности: 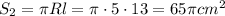S_2= \pi Rl= \pi \cdot5\cdot 13=65 \pi cm^{2}

Соответственно площадь полн. поверхности: 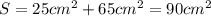S=25 cm^{2} +65cm^{2} = 90 cm^{2}

Объём конуса: 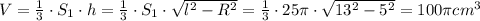V= \frac{1}{3} \cdot S_1\cdot h= \frac{1}{3} \cdot S_1\cdot \sqrt{l^2-R^2} = \frac{1}{3} \cdot25 \pi \cdot \sqrt{13^2-5^2} =100 \pi cm^{3}

Nastya8laif
Nastya8laif
4,8(75 оценок)

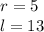
r = 5 \\ l = 13

Найти:

1) V - объем конуса

2) S - площадь полной поверхности конуса

1) Найдем объем конуса V с формулы:

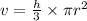
v = \frac{h}{3} \times \pi {r}^{2}

Найдем h - высоту с теоремы Пифагора:

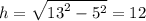
h = \sqrt{ {13}^{2} - {5}^{2} } = 12

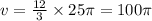
v = \frac{12}{3} \times 25\pi = 100\pi

2) Объем нашли, теперь найдем площадь полной поверхности S:

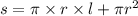
s = \pi \times r \times l + \pi {r}^{2}

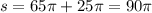
s = 65\pi + 25\pi = 90\pi

V = 100π; S=90π

VPVolkov03
VPVolkov03
4,4(25 оценок)
1) -4x+x< 7+8 -3x< 15 x> -5 2) -8x+4x< 3+9 -4x< 12 x> -3 3) 4x-9x< 7+5 -5x< 12 x> -2,4 4) 8x-7x> 6+20 x> 26 5) -3x-7x> -10-15 -10x> -25 x< 2,5 6) 7x+3x< 6+2 10x< 8 x< 0,8 7)2x+2x> 9-3 4x> 6 x> 1,5

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS