Dertylt

11.02.2020 23:25

Геометрия

Есть ответ 👍

Сторона основания правильной треугольной пирамиды равна 72 м, боковое ребро с плоскостью основания образует угол 30°. Вычисли высоту пирамиды.

283

411

Посмотреть ответы 2

Ответы на вопрос:

Direct228

Геометрия

4,7(86 оценок)

ответ: ДО=8√3см

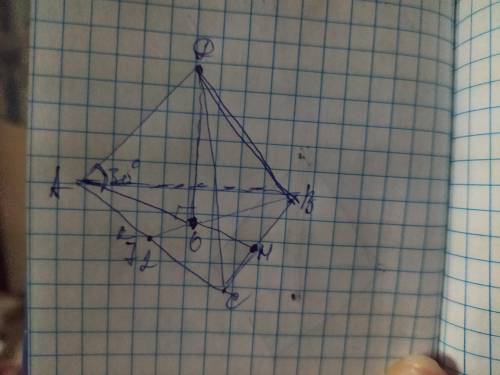
Объяснение: обозначим вершины основания пирамиды А В С, вершину пирамиды Д, а её высоту ДО. В основании правильной трёхугольной пирамиды лежит равносторонний треугольник, поэтому АВ=ВС=АС=72м

Найдём площадь основания по формуле:

S=a²√3/4,где а- сторона основания:

S=72²√3/4=5184//√3/4=1296√3см²

S=1296см².

Проведём из вершин основания медианы АН и ВК. Они пересекаясь в точке О делятся между собой в отношении 2:1, начиная от вершины треугольника: АО: ОН=2:1. Также медиана является ещё и высотой, поскольку треугольник равносторонний. Найдём высоту основания через площадь следуя формуле обратной формуле площади:

S=½×a×h

h=S÷a÷½=1296÷72÷½=18×2=36см

h=36см

Обозначим пропорции 2:1 как 2х и х, и зная величину высоты, составим уравнение:

2х+х=36

3х=36

х=36/3

х=12

ОН=12см, тогда АО=12×2=24см.

Рассмотрим ∆АДО. Он прямоугольный где АО и ДО- катеты, а АД- гипотенуза. Угол ДАО=30°, по условиям, а катет лежащий напротив него равен половине гипотенузы, поэтому ДО=½× АД

Пусть ДО=х, тогда АД=2х, зная, что АО=24см, составим уравнение используя теорему Пифагора:

АД²-ДР²=АО²

(2х)²-х²=24²

4х²-х²=576

3х²=576

х²=576/3

х²=192

х=√192=√(3×64)=8√3

Итак: ДО=8√3см

Сторона основания правильной треугольной пирамиды равна 72 м, боковое ребро с плоскостью основания о

sukhovershaya

Геометрия

4,4(94 оценок)

c перпеникулярна b вроде так

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.