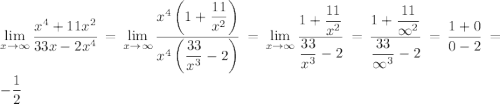Ответы на вопрос:
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Математика
-
При каких значениях х равны значения выражений 2*(0.6 - 2х) и 1.2 + 4х...
 SashaZaisnik124.01.2021 09:43
SashaZaisnik124.01.2021 09:43 -
Люди а) 1,75: 1,4 б) 25,9: 3,7 в)86,1: 2,46 г)18,4: 7,36 заранее и 10 ваши...
 timon04080510.03.2022 19:58
timon04080510.03.2022 19:58 -
Какое число нужно разделить на 9 чтобы получился 0?...
 06Loki9026.01.2023 00:02
06Loki9026.01.2023 00:02 -
Выбирите наименьшее из чисел 1,3; 1,25; 1/3...
 Alina2251123.06.2021 21:25
Alina2251123.06.2021 21:25 -
Сократите дробь: 7*8/4*15; ,объясните как решить)!...
 LavaGuy11111.04.2022 10:13
LavaGuy11111.04.2022 10:13 -
Запиши разность числа 3 и а. найди значения выражения если а=3; 0....
 пупсень624.05.2022 20:54
пупсень624.05.2022 20:54 -
Мастерская школы 120 книг переплел за 4 дня.если будет так работать,то 480 книг...
 sonikzets04.04.2022 12:14
sonikzets04.04.2022 12:14 -
Что означает например: я навязываюсь с тобой дружить? скажите . заранее...
 Mariaaria2260416.11.2021 03:07
Mariaaria2260416.11.2021 03:07 -
Вычисли разными способами 25*11; 236*11; 3245*11; 4236*11;...
 artemlis130220012.07.2021 20:43
artemlis130220012.07.2021 20:43 -
Какое число нужно разделить на 9,чтобы получился ноль и остаток 8?...
 parvizmirzoev0323.03.2021 15:25
parvizmirzoev0323.03.2021 15:25

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.