Покажите, что электромагнитное поле, выраженное уравнениями Ex=Ey=0; Ez=cos(y-ct); Bx= cos(y-ct); By=Bz=0 удовлетворяет уравнения Максвелла в пустом пространстве.

159

416

Посмотреть ответы 2

Ответы на вопрос:

NaraDarkTheHelp

Физика

4,4(75 оценок)

Рассмотрим уравнения Максвелла в дифференциальной форме, нам понадобятся 3 и 4 уравнения:

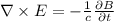
$\nabla \times E=-\frac{1}{c} \frac{\partial B}{\partial t}$

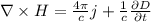
$\nabla \times H=\frac{4\pi }{c} j+\frac{1}{c} \frac{\partial D}{\partial t}$

Найдем ротор вектора напряженности по известным его компонентам:

$\nabla \times E=\left[\begin{array}{ccc}i&j&k\\\frac{\partial }{\partial _x} &\frac{\partial }{\partial _y}&\frac{\partial }{\partial _z}\\E_x&E_y&E_z\end{array}\right]=\left[\begin{array}{ccc}i&j&k\\\frac{\partial }{\partial _x} &\frac{\partial }{\partial _y}&\frac{\partial }{\partial _z}\\0&0&cos(y-ct)\end{array}\right] =i*-sin(y-ct)$

Найдем производную магнитной индукции по времени:

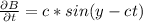
$\frac{\partial B}{\partial t} =c*sin(y-ct)$

Действительно, легко видеть что они удовлетворяют третьему уравнению.

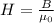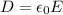
Теперь найдем ротор вектора напряженности магнитного поля, учитывая что $H=\frac{B}{\mu _0}$ и $D=\epsilon_0 E$

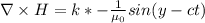
$\nabla\times H=k*-\frac{1}{\mu_0} sin(y-ct)$

Производная электрической индукции по времени:

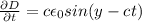
$\frac{\partial D}{\partial t}=c \epsilon_0 sin(y-ct)$

Но так как 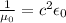$\frac{1}{\mu_0}=c^2\epsilon_0$ ротор напряженности магнитного поля также совпадает с производной электрической индукции по времени, деленной на скорость света (для электромагнитной волны плотность тока j считаем нулевой, так как нет среды проводимости).

ggf6fr

Физика

4,4(2 оценок)

e=k*q/r² увеличится в 6 раз

===============

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Физика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.