Lana8254

11.01.2023 04:55

Геометрия

Есть ответ 👍

Составить уравнение плоскости проходящей через точки L(0,0,1) и N(3,0,0) и образующей угол в 60° с плоскостью (ху объясните подробнее

220

230

Посмотреть ответы 2

Ответы на вопрос:

MikiMio

Геометрия

4,5(83 оценок)

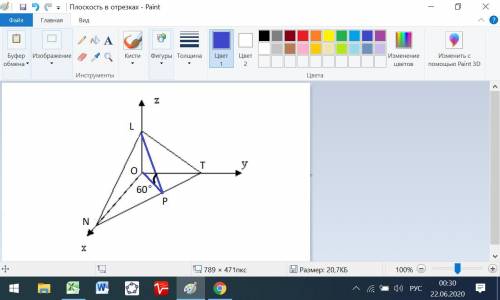
Даны точки L(0,0,1) и N(3,0,0) и угол в 60° с плоскостью (ху).

Плоский угол лежит в плоскости, перпендикулярной к линии пересечения. Это угол LPO.

ОР = 1/tg 60° = 1/√3.

NP = √(3² - (1/√3)²) = √(9 - (1/3) = √(26/3).

Из подобия треугольников находим:

NP/ON = OP/OT.

Получаем ОТ = 3/√26.

Теперь имеем 3 точки и по ним определяем уравнение плоскости.

Для составления уравнения плоскости используем формулу:

x - xA y - yA z - zA

xB - xA yB - yA zB - zA

xC - xA yC - yA zC - zA

= 0

Подставим данные и упростим выражение:

x - 3 y - 0 z - 0

0 - 3 0 - 0 1 - 0

0 - 3 0.588348405 - 0 0 - 0

= 0

x - 3 y - 0 z - 0

-3 0 1

-3 0.588348405 0

= 0

x - 3 0·0-1·0.588348405 - y - 0 (-3)·0-1·(-3) + z - 0 (-3)·0.588348405-0·(-3) = 0

(-0.588348405) x - 3 + (-3) y - 0 + (-1.765045215) z - 0 = 0

- 0.588348405x - 3y - 1.765045215z + 1.765045215 = 0 .

Можно представить коэффициенты уравнения в радикалах.

(-3/√26)x - 3y - (9/√26)z + (9/√26) = 0.

Составить уравнение плоскости проходящей через точки L(0,0,1) и N(3,0,0) и образующей угол в 60° с п

kristina200614

Геометрия

4,5(57 оценок)

(-2; 3)

Объяснение:

Центром исходной окружности является точка с координатами (2;3).

Проводим перпендикуляр к оси ординат, а потом такой же от нее и получаем т с координатами (-2; 3)

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.