romakim02kum

09.04.2020 12:50

Геометрия

Есть ответ 👍

Стороны основания правильной треугольной пирамиды 5 см, высота пирамиды равна 10 см. Найти полную поверхность пирамиды

133

486

Посмотреть ответы 2

Ответы на вопрос:

Кристинанана

Геометрия

4,6(3 оценок)

Дано:

Правильная треугольная пирамида.

AB = 5 см.

MO = 10 см.

Найти:

S полн. поверх. = ? см².

Решение:

Так как данная пирамида - правильная, треугольная ⇒ основание этой пирамиды - равносторонний треугольник.

Равносторонний треугольник - это треугольник, у которого все стороны и углы равны.

⇒ AB = BC = CA = 5 см.

Проведём из вершины M к основанию правильной треугольной пирамиды апофему MK.

Апофема - высота боковой грани правильной пирамиды, проведённая из вершины этой пирамиды.

Апофема, проведённая к стороне основания правильной треугольной пирамиды, делит эту сторону пополам.

⇒ CK = KB = 5/2 = 2,5 см.

Катет прямоугольного треугольника, образованный апофемой пирамиды, высотой и отрезком, их соединяющим, равен половине длины основания правильной треугольной пирамиды.

⇒ CK = KB = KO = 2,5 см.

Найдём апофему МК, по теореме Пифагора (c = √(a² + b²), где c - гипотенуза, a, b - катеты):

MK = √(MO² + KO²) = √(10² + 2,5²) = √(100 + 6,25) = √106,25 = (5√17)/2 см.

P основ. = P ΔABC = AB + BC + CA = 5 + 5 + 5 = 5 · 3 = 15 см.

S бок. поверх. = 1/2 · P · MK = 1/2 · 15 · (5√17)/2 = (75√17)/4 см².

S основ. = S ΔABC = (a²√3)/4 = (5²√3)/4 = (25√3)/4 см².

S полн. поверх. = S основ. + S бок. поверх.

⇒ S полн. поверх. = (25√3)/4 + (75√17)/4 = 25/4 · (3√17 + √3) см².

ответ: S полн. поверх. = 25/4 · (3√17 + √3) см².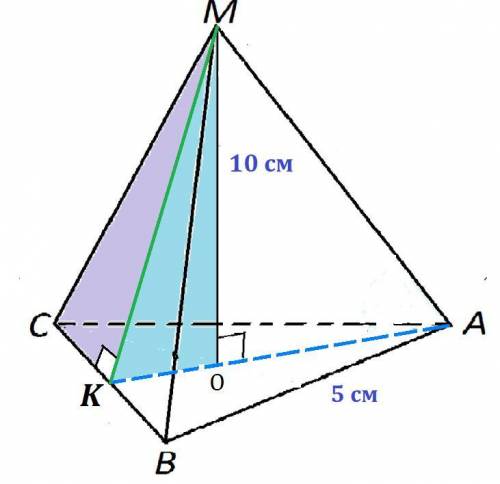
Стороны основания правильной треугольной пирамиды 5 см, высота пирамиды равна 10 см. Найти полную по

slava02555

Геометрия

4,6(97 оценок)

значит r- 15

S.ABCD-48

Объяснение:

типо умножь

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.