Регистрация Спросить otvet5GPT
albinka2017
25.04.2021 01:49
Алгебра
Есть ответ 👍

Найдите область определения функции. ------------------------------------------------------------- Огромное распишите каждое действие в решении выражения, желательно через встроенную среду написания математики в знаниях. Кидать ответ с фотомача для набора - 1 звезда и жалоба. --------------------------------------------------------------

168
404
Посмотреть ответы 2

Ответы на вопрос:

Соня121103
Соня121103
4,6(25 оценок)

Первое, что можем заметить, это то, что выражение под корнем больше/равно нулю. Также замечаем, что знаменатель в дробовом выражении не может равняться нулю (Это записывать не нужно, так как будет включаться в решение неравенства).

Решим неравенство:

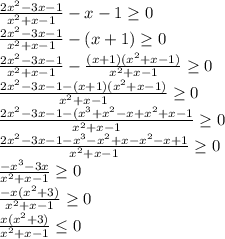
\frac{2x^{2}-3x-1}{x^{2}+x-1} -x-1 \geq 0\\\frac{2x^{2}-3x-1}{x^{2}+x-1} - (x+1) \geq 0\\\frac{2x^{2}-3x-1}{x^{2}+x-1} - \frac{(x+1)(x^{2}+x-1)}{x^{2}+x-1} \geq 0\\\frac{2x^{2}-3x-1-(x+1)(x^{2}+x-1)}{x^{2}+x-1} \geq 0\\\frac{2x^{2}-3x-1-(x^{3}+x^{2}-x+x^{2}+x-1}{x^{2}+x-1} \geq 0\\\frac{2x^{2}-3x-1-x^{3}-x^{2}+x-x^{2}-x+1}{x^{2}+x-1} \geq 0\\\frac{-x^{3}-3x}{x^{2}+x-1} \geq 0\\\frac{-x(x^{2}+3)}{x^{2}+x-1} \geq 0\\\frac{x(x^{2}+3)}{x^{2}+x-1} \leq 0\\

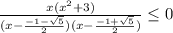
\frac{x(x^{2}+3)}{(x - \frac{-1-\sqrt{5}}{2})(x - \frac{-1+\sqrt{5}}{2})} \leq 0

Отсюда имеем решение (значит и область определения):

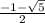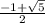x∈( -∞ ; \frac{-1-\sqrt{5}}{2} ) ∪ [ 0 ; \frac{-1+\sqrt{5}}{2} )

Griezman7
Griezman7
4,4(25 оценок)

В решении

Объяснение:

Выразите х из каждого равенства :

1) 6х+4а-х+7b=8а+6b

Привести подобные члены:

5х + 4а + 7b = 8a + 6b

Перенести х в левую часть, остальное в правую:

5х = 8a + 6b - 4a - 7b

Привести подобные члены в правой части:

5х = 4a - b

Выразить х:

х = (4a - b)/5.

2) 7х-8а-4х-9b=4a-6b

Схема решения та же:

3х - 8a - 9b = 4a - 6b

3x = 4a - 6b + 8a + 9b

3x = 12a + 3b

x = (12a + 3b)/3

x = 4a + b.

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS