Регистрация Спросить otvet5GPT
Алина051206
21.01.2023 14:08
Физика
Есть ответ 👍

Здравствуйте решить предложенную задачу. Пластинки из разных сортов стекла одинаковой толщины прижаты вплотную друг к другу. На верхнюю пластинку свет падает под углом а = 53 градуса . Во сколько раз различаются времена прохождения света через эти пластинки? Показатель преломления верхней пластины n1 = 1,4, а нижней n2 = 2,0. Считать sin 53 = 0,8; сos53 = 0,6

268
399
Посмотреть ответы 2

Ответы на вопрос:

РевинаМелек
РевинаМелек
4,6(32 оценок)

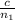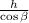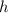Скорость световой волны при прохождении первой пластинки равна \frac{c}{n_{1}}, считая, что она идет из воздуха. Длина пути составляет \frac{h}{\cos\beta}, где h — толщина пластинки, 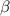\beta — угол преломления. Этот же угол является углом падения на вторую пластинку. 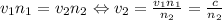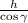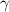Скорость световой волны при прохождении второй пластинки можно найти из уравнения: v_{1}n_{1}=v_{2}n_{2} \Leftrightarrow v_{2}=\frac{v_{1}n_{1}}{n_{2}}=\frac{c}{n_{2}}, длина пути — \frac{h}{\cos\gamma}, где \gamma — угол преломления.

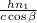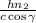Время прохождения первой пластинки: \frac{hn_{1}}{c\cos\beta}, второй: \frac{hn_{2}}{c\cos\gamma}.

Искомое отношение равно 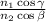\frac{n_{1}\cos\gamma}{n_{2}\cos\beta}. При этом 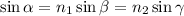\sin\alpha=n_{1}\sin\beta=n_{2}\sin\gamma. Отношение будет иметь вид:  

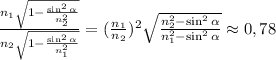
\frac{n_{1}\sqrt{1-\frac{\sin^{2}\alpha}{n_{2}^2} } }{n_{2}\sqrt{1-\frac{\sin^{2}\alpha}{n_{1}^2} } } =(\frac{n_{1}}{n_{2}})^2\sqrt{\frac{n_{2}^2-\sin^{2}\alpha}{n_{1}^2-\sin^2\alpha }} \approx 0,78

DanilkaMare
DanilkaMare
4,5(90 оценок)

a) 30 мин.=0.5ч, за полчаса конец минутной стрелки пройдет путь, равный половине   длины окружности, т.е. 2πr/2≈3.14*10=31.4/cм/

модуль перемещения равен двум радиусам 2*10=20/см/

б) расстояние равно 2πr, 2*3.14*10=62.8/см/

а путь равен нулю. т.к. через 2 часа конец стрелки вернется в исходное положение, т.е. в точку начала движения.

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Физика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS