Алгебра: Докажите классическое неравенство:

vasifalieyev001

27.08.2020 13:32

Алгебра

Есть ответ 👍

Докажите классическое неравенство: $\frac{2}{\frac{1}{a} +\frac{1}{b} } \leq \sqrt{ab}$

139

177

Посмотреть ответы 3

Ответы на вопрос:

Ramazan1403

Алгебра

4,6(34 оценок)

(см. объяснение)

Объяснение:

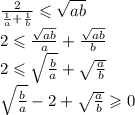
$\frac{2}{ \frac{1}{a} + \frac{1}{b} } \leqslant \sqrt{ab} \\ 2 \leqslant \frac{ \sqrt{ab} }{a} + \frac{ \sqrt{ab} }{b} \\ 2 \leqslant \sqrt{ \frac{b}{a} } + \sqrt{ \frac{a}{b} } \\ \sqrt{ \frac{b}{a} } - 2+ \sqrt{ \frac{a}{b} } \geqslant 0$

Рассмотрим внимательно получившееся выражение: это формула сокращённого умножения: разность квадратов. Учитывая это, перепишем выражение:

$( \sqrt[4]{ \frac{b}{a} } - \sqrt[4]{ \frac{a}{b} } ) {}^{2} \geqslant 0$

Выражение в квадрате всегда не отрицательно, поэтому равенство выше всегда верно.

Доказано.

raykova568

Алгебра

4,5(27 оценок)

Объяснение:

Для отрицательных a и b неравенство очевидно. Докажем для случая a,b>0:

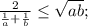
$\frac{2}{\frac{1}{a}+\frac{1}{b}} \leq \sqrt{ab};$

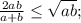
$\frac{2ab}{a+b} \leq \sqrt{ab};$

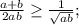
$\frac{a+b}{2ab}\geq \frac{1}{\sqrt{ab}};$

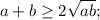
$a+b \geq 2\sqrt{ab};$

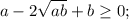
$a-2\sqrt{ab}+b\geq 0;$

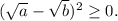
$(\sqrt{a}-\sqrt{b})^2\geq0.$

Последнее неравенство выполняется для любых неотрицательных a и b, что с учетом ОДЗ исходного неравенства говорит о том, что оно справедливо для любых положительных a и b, причем равенство достигается при a=b>0

2o2o

Алгебра

4,6(37 оценок)

1)100%-25%=75%=0.75

2)810:0.74=1080р

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.