alinika2007

26.01.2023 19:14

Математика

Есть ответ 👍

Нужно найти частные производные функции z=ctg(x+y). Не очень понимаю, как делать

125

244

Посмотреть ответы 2

Ответы на вопрос:

sashazen03

Математика

4,8(1 оценок)

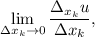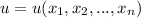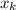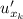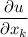
Если существует предел $\displaystyle \lim_{\Delta x_{k} \to 0}\dfrac{\Delta_{x_{k}}u}{\Delta x_{k}},$ то этот предел называется частной производной от функции $u = u(x_{1}, x_{2}, ..., x_{n})$ по переменной $x_{k}$ и обозначается $u'_{x_{k}}$ или $\dfrac{\partial u}{\partial x_{k}}$

Для функции 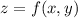z = f(x, y) следует найти частные производные 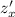$z'_{x}$ и $z'_{y}$

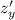
Для нахождения таких производных по данной переменной следует все переменные, кроме данной, считать константами (числами).

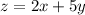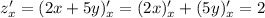Например, для функции z = 2x + 5y частной производной функции по переменной будет: $z'_{x} = (2x + 5y)'_{x} = (2x)'_{x} + (5y)'_{x} = 2$ (считаем выражение 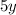числовым, производная от которого равна нулю), и аналогично по переменной 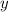будет: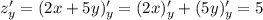 $z'_{y} = (2x + 5y)'_{y} = (2x)'_{y} + (5y)'_{y} = 5$

Для заданной функции 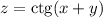$z = \text{ctg} (x + y)$ найдем частные производные 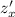$z'_{x}$ и $z'_{y}$

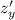
Воспользуемся формулой 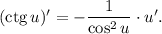$(\text{ctg} \, u)' = -\dfrac{1}{\cos^{2}u} \cdot u'.$

Имеем:

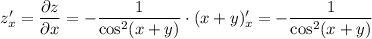
$z'_{x} = \dfrac{\partial z}{\partial x} = -\dfrac{1}{\cos^{2}(x + y)} \cdot (x + y)'_{x} = -\dfrac{1}{\cos^{2}(x + y)}$

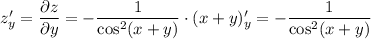
$z'_{y} = \dfrac{\partial z}{\partial y} = -\dfrac{1}{\cos^{2}(x + y)} \cdot (x + y)'_{y} = -\dfrac{1}{\cos^{2}(x + y)}$

ответ: 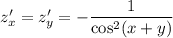$z'_{x} = z'_{y} = -\dfrac{1}{\cos^{2}(x + y)}$

Molina121212

Математика

4,6(64 оценок)

9•(7•5)=(9•7)•5 8•(6•3)=(8•6)•3

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.