Математика: HELP! Исследовать сходимость числового ряда!

Tatarin570

19.04.2023 21:21

Математика

Есть ответ 👍

HELP! Исследовать сходимость числового ряда!

235

419

Посмотреть ответы 2

Ответы на вопрос:

djonli1

Математика

4,6(82 оценок)

Ряд сходится, но не сходится абсолютно

Пошаговое объяснение:

Домножим каждый член ряда на 3, от этого сходимость не поменяется, так что с этого места считаем, что 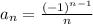$a_n = \frac{(-1)^{n - 1}}{n}$ .

Заметим, что ряд составленный из 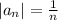$|a_n| = \frac{1}{n}$ является гармоническим рядом, который, как известно, расходится. Поэтому ряд не сходится абсолютно. Чтобы доказать просто сходимость, разобьем слагаемые попарно:

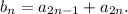
$b_n = a_{2n - 1} + a_{2n}.$

Заметим, что

$b_n = a_{2n - 1} + a_{2n} = \frac{1}{2n - 1} - \frac{1}{2n} = \frac{1}{2n(2n - 1)} \leq \frac{1}{4n^2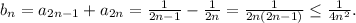}.$ Заметим, что ряд составленный из 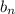b_n сходится, так как он составлен из положительных членов и мажорируется сходящимся рядом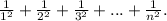 $\frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + ... + \frac{1}{n^2}.$

Обозначим частичные суммы ряда 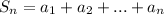S_n = a_1 + a_2 + ... + a_n .

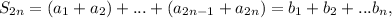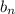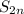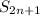Тогда в наших обозначения $S_{2n} = (a_1 + a_2) + ... + (a_{2n - 1} +a_{2n}) = b_1 + b_2 + ... b_n,$ а ряд из b_n сходится, значит $S_{2n}$ имеет предел. Обозначим этот предел за . Для окончания доказательства, докажем что частичные суммы $S_{2n + 1}$ тоже сходятся к a.

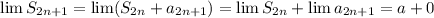$\lim S_{2n + 1} = \lim (S_{2n} + a_{2n + 1}) = \lim S_{2n} + \lim a_{2n + 1} = a + 0$ , так как очевидно, что 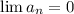$\lim a_{n} = 0$ . Итого, мы доказали, что у частичных сумм есть предел , значит ряд сходится по определению

sofyagorobecmaozu3v3

Математика

4,4(87 оценок)

4÷2 2/3=4/1÷8/3=4/1×3/8=12/8=3/2=1,5

ответ: 1,5 (ну или 3/2)

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.