Регистрация Спросить otvet5GPT
arslando
26.06.2021 02:17
Математика
Есть ответ 👍

решить уравнение: 4cos2x – sin x -1 = 0

156
458
Посмотреть ответы 3

Ответы на вопрос:

staylent
staylent
4,4(12 оценок)

(см. объяснение)

Пошаговое объяснение:

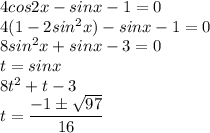
4cos2x-sin x -1 = 0\\4(1-2sin^2x)-sinx-1=0\\8sin^2x+sinx-3=0\\t=sinx\\8t^2+t-3\\t=\dfrac{-1\pm\sqrt{97}}{16}

Откуда получаем 2 уравнения:

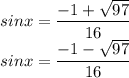
sinx=\dfrac{-1+\sqrt{97}}{16}\\sinx=\dfrac{-1-\sqrt{97}}{16}

Откуда получаем ответ:

x_1=\arcsin\left(\dfrac{-1+\sqrt{97}}{16}\right)+2n\pi,\;n\in \mathbb{Z}\\x_2=\pi-\arcsin\left(\dfrac{-1+\sqrt{97}}{16}\right)+2n\pi,\;n\in \mathbb{Z}\\x_3=-\arcsin\left(\dfrac{1+\sqrt{97}}{16}\right)+2n\pi,\;n\in \mathbb{Z}\\x_4=\pi+\arcsin\left(\dfrac{1+\sqrt{97}}{16}\right)+2n\pi,\;n\in \mathbb{Z}

Уравнение решено!

Шпунтик99
Шпунтик99
4,8(97 оценок)

4cos2x – sin x -1 = 0

Представим cos2x как 1-sin²x, тогда

4*(1-sin²x) – sin x -1 = 0

4 - 4sin²x – sin x -1 = 0

- 4sin²x – sin x + 3 = 0 | : (-1)

4sin²x + sin x - 3 = 0

Пусть sin x = t , тогда

4t² + t - 3 = 0

D = 1² - 4 * 4 * (-3) = 1 + 48 = 49 = 7²

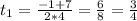
t_{1} = \frac{-1+7}{2*4} = \frac{6}{8} = \frac{3}{4}

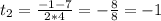
t_{2} = \frac{-1-7}{2*4} = -\frac{8}{8} = -1

Вернёмся к замене:

sin x = 3/4

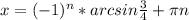x = (-1)^{n} * arcsin \frac{3}{4} + \pi n , n∈Z

sin x = -1

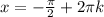x = - \frac{\pi }{2} + 2\pi k, k∈Z

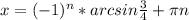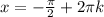ответ: x = (-1)^{n} * arcsin \frac{3}{4} + \pi n, n∈Z ; x = - \frac{\pi }{2} + 2\pi k, k∈Z .

texin508
texin508
4,8(48 оценок)

3660 секунд

Пошаговое объяснение:

1 * 3600 + 1 * 60 = 3660 секунд

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS