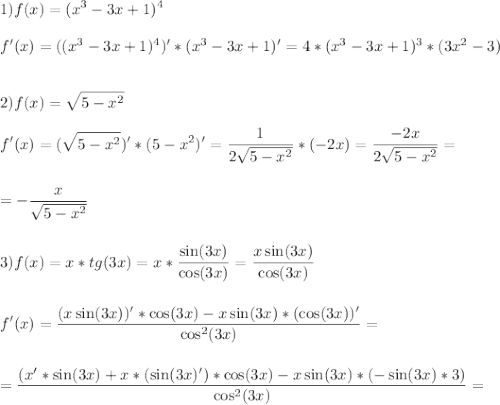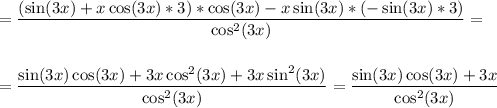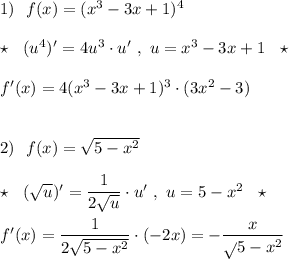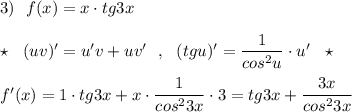Найти производную функций 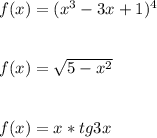 Очень нужно свериться.Решение с онлайн калькуляторов не предлагайте.
Очень нужно свериться.Решение с онлайн калькуляторов не предлагайте.
231
392
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
Спростити вираз в дужках (8 - 2x)(2+x)+(x-2)(4+2x) . Обчислити , якщо x=2 до іть...
 маришка21317.05.2022 03:27
маришка21317.05.2022 03:27 -
Сиделать на листке очень без...
 savelevad12003.06.2022 03:54
savelevad12003.06.2022 03:54 -
Определи, правее каких чисел на этом луче будут 84−−√ и 53−−√? В ответе укажи ближайшее...
 Nikitoskin10225.07.2020 13:28
Nikitoskin10225.07.2020 13:28 -
Коарденальный модуль A2 весит в 2 раза больше чем модуль В5 а модусь С8 на 300 г...
 Haranmeu31.10.2021 07:30
Haranmeu31.10.2021 07:30 -
1. Заполните кластер. Виды изображения местности...
 сяньчик17.06.2020 07:16
сяньчик17.06.2020 07:16 -
Вычитание трех квадратичных членов на множители а квадрат+6а+8 ...
 Poligrinka08.04.2022 18:53
Poligrinka08.04.2022 18:53 -
Сравни числа корень 17 и корень 18...
 justnastasyaaa22.07.2021 15:33
justnastasyaaa22.07.2021 15:33 -
Срешением и объяснением 1)2^2x-6*2^x+8=0 2)3^2x-6*3^x-27=0...
 wwwcom104.05.2021 16:10
wwwcom104.05.2021 16:10 -
Решите систему уравнений методом сложения (3х+2у=3 (2х+5у=13...
 fullwalkgroundEger11.04.2022 12:02
fullwalkgroundEger11.04.2022 12:02 -
решить задачу с сложения или умножения числовых неравенств. Купили 4 общие тетради...
 edbaldin201706.05.2022 07:08
edbaldin201706.05.2022 07:08

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.