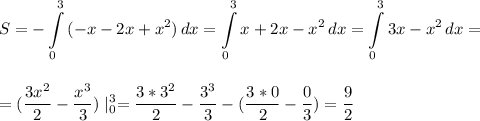Математика: Найти площадь фигуры, ограниченной кривыми y=2x-x^2 и x+y=0

123321456654sego

22.04.2021 08:24

Математика

Есть ответ 👍

Найти площадь фигуры, ограниченной кривыми
y=2x-x^2 и x+y=0

237

401

Посмотреть ответы 3

Ответы на вопрос:

Skrilleax95

Математика

4,7(36 оценок)

Пошаговое объяснение:

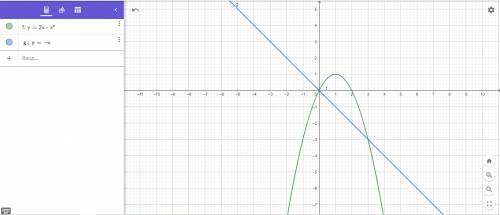
площадь фигуры равна определенному интегралу от разницы у₁(х) - у₂(х),

пределы интегрирования - это точки пересечения функций

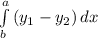
$\int\limits^a_b {(y_{1} -y_{2} } )\, dx$

напишем формулы в удобном виде

у₁ = 2х - х²

у₂ = -х

найдем точки пересечения функций

2х -х² = -х

х²-2х -х =0 ⇒ х²-3х = 0 ⇒ х(х-3) = 0 ⇒ х₁ = 0, х₂ = 3

это есть точки, где графики пересекаются, и эти же значения есть пределы интегрирования

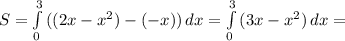
$S = \int\limits^3_0 {((2x-x^{2}) -(-x)) } \, dx = \int\limits^3_0 {(3x -x^{2} )} \, dx =$

интеграл разности равен разности интегралов. константу выносим за знак интеграла. получим

$= 3\int\limits^3_0 {x} \, dx - \int\limits^3_0 {x^{2} x} \, dx =\left[\begin{array}{ccc}\int\limits {x^{2} } \, dx =\frac{x^{3} }{3} \\\int\limits {x} \, dx = \frac{x^{2} }{2} \\\end{array}\right] =$

здесь в скобках указаны табличные интегралы. ими и воспользуемся

(3х² / 2) Ι₀³ - (х³/3) Ι₀³ = -9 + 27/2 = 9/2

S = 9/2

kdortskaya55

Математика

4,6(60 оценок)

$\displaystyle\\S=-\int\limits^3_0 {(-x-2x+x^2)} \, dx=\int\limits^3_0 {x+2x-x^2} \, dx =\int\limits^3_0 {3x-x^2} \, dx=\\\\\\=(\frac{3x^2}{2}-\frac{x^3}{3})\mid^3_0=\frac{3*3^2}{2}-\frac{3^3}{3}-(\frac{3*0}{2}-\frac{0}{3})=\frac{9}{2}$

Найти площадь фигуры, ограниченной кривыми y=2x-x^2 и x+y=0

1220051404

Математика

4,8(14 оценок)

17 4/7

Пошаговое объяснение:

(2 1/2+1 1/3) : 1/6-5 3/7= (15/6+8/6) : 1/6-5 3/7=23/6 : 1/6 - 5 3/7= 23 -5 3/7=17 4/7

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.