Геометрия: Неужели геометрия как и мне никому не даётся???( >

Маша10578

02.03.2020 05:02

Геометрия

Есть ответ 👍

Неужели геометрия как и мне никому не даётся???(">

292

369

Посмотреть ответы 3

Ответы на вопрос:

sever174

Геометрия

4,8(78 оценок)

(Ах да, простите, явно не 15 минут

(Можно только 5 файлов загрузить, пришлось два последних склеить :) )

Неужели геометрия как и мне никому не даётся???(

Ani32536

Геометрия

4,7(62 оценок)

а) Доказано; б) 36

Объяснение:

а)

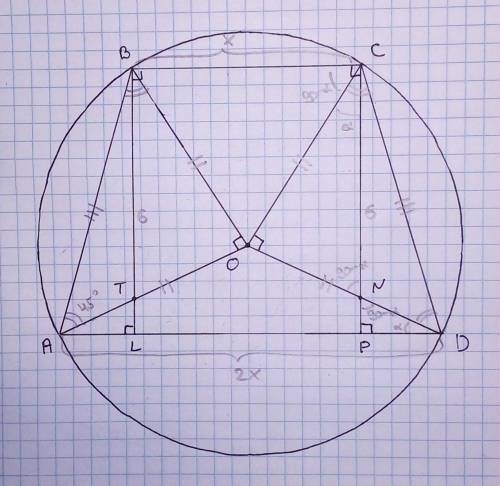
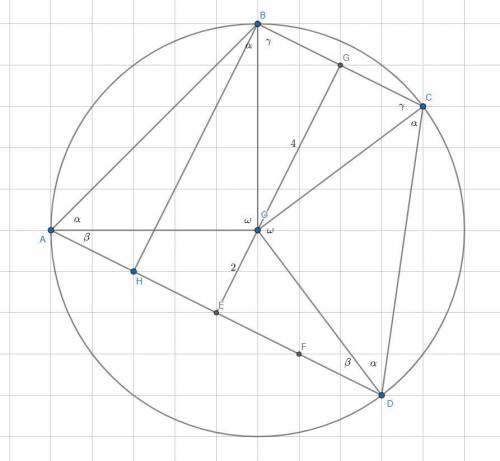
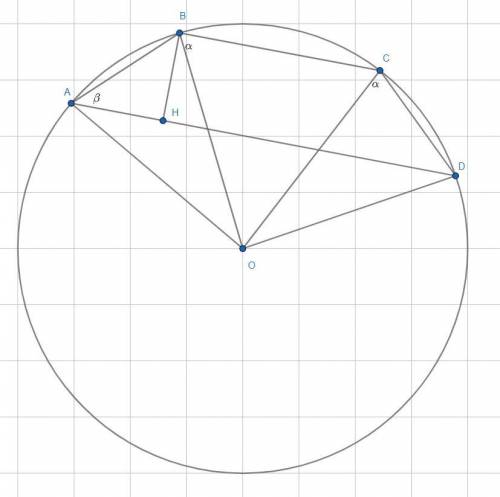
Обратимся к первому рисунку. Пусть ∠AOB=∠COD=ω. Тогда ∠BAO=∠ABO=∠OCD=∠ODC=α (AO=OB=R и CO=OD=R => треугольники ABO и COD равнобедренные, в которых угол против основания общий, а => 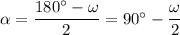$\alpha=\dfrac{180^\circ-\omega}{2}=90^\circ-\dfrac{\omega}{2}$ ). ΔAOD равнобедренный (AO=OD=R) => ∠OAD=∠ODA=β. Аналогично ∠OBC=∠OCB=γ. Т.к. четырехугольник вписан в окружность, то ∠BAD+∠BCD=180°. Значит: 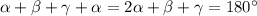$\alpha+\beta+\gamma+\alpha=2\alpha+\beta+\gamma=180^\circ$ . ∠BAD+∠ABC= 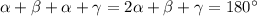$\alpha+\beta+\alpha+\gamma=2\alpha+\beta+\gamma=180^\circ$ . Получили, что 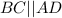BC||AD , т.к. внутренние односторонние углы при этих прямых и секущей AB в сумме дают 180°. Поскольку AD≠BC (по условию AD=2BC), четырехугольник трапеция, а не параллелограмм, а так как она вписана в окружность, то равнобедренная. Доказано.

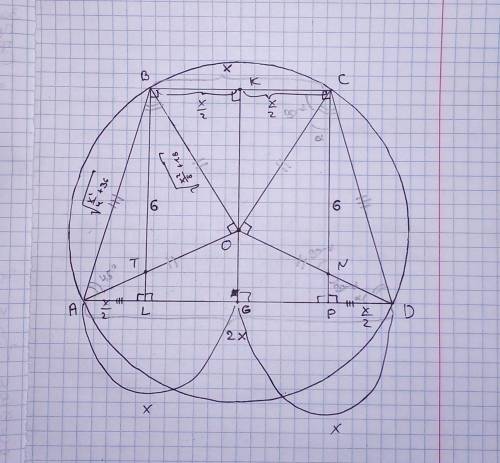
Заметим, что центр описанной около четырехугольника окружности может лежать вне него. Тогда доказательство будет отличаться. Начиная с этого момента забудем о тех обозначениях, которые были введены для доказательства первого случая. Обратимся ко второму рисунку. Заметим, что ∠ABC=∠BCD=α, так как AO=OB=R и CO=OD=R => треугольники ABO и COD равнобедренные, в которых угол против основания общий, а => 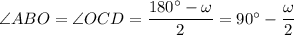$\angle ABO=\angle OCD=\dfrac{180^\circ-\omega}{2}=90^\circ-\dfrac{\omega}{2}$ (здесь ∠AOB=∠COD=ω) и ∠OBC=∠BCO, так как это углы при основании равнобедренного треугольника BOC (OB=OC=R). Пусть ∠BAD=β. Тогда 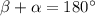$\beta+\alpha=180^\circ$ (так как четырехугольник вписанный). Но 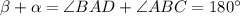$\beta+\alpha=\angle BAD+\angle ABC=180^\circ$ . Значит 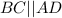BC||AD , т.к. внутренние односторонние углы при этих прямых и секущей AB в сумме дают 180°. Поскольку AD≠BC (по условию AD=2BC), четырехугольник трапеция, а не параллелограмм, а так как она вписана в окружность, то равнобедренная. Доказано.

б)

Решим задачу для 1-ого случая:

Пусть EG - расстояние между прямыми BC и AD. Т.к. BC||AD, то EG=6. Заметим, что треугольники BOC и AOD равновеликие.

Докажем это:

Пусть ∠BOC=α. Тогда (так как ∠AOB=∠COD=90°, а => ∠BOC+∠AOD=360°-90°-90°=180°) ∠AOD=180°-α.

Получим:

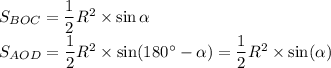
$S_{BOC}=\dfrac{1}{2}R^2\times\sin\alpha\\S_{AOD}=\dfrac{1}{2}R^2\times\sin(180^\circ-\alpha)=\dfrac{1}{2}R^2\times\sin(\alpha)$

Запишем их площади через формулу про основание и высоту:

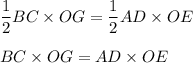
$\dfrac{1}{2}BC\times OG=\dfrac{1}{2}AD\times OE\\\\BC\times OG=AD\times OE$

Из условия следует, что AD=2BC.

Тогда:

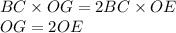
$BC\times OG=2BC\times OE\\OG=2OE$

Знаем, что:

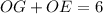
OG+OE=6

Тогда:

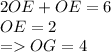
$2OE+OE=6\\OE=2\\=OG=4$

Поскольку треугольники BOC и AOD равнобедренные, то OG и OE не только их высоты, но и медианы соответственно, а значит BG=BC/2 и AE=AD/2.

Тогда из прямоугольных треугольников BOG и AOE по теореме Пифагора найдем BC и AD:

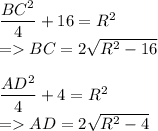
$\dfrac{BC^2}{4}+16=R^2\\=BC=2\sqrt{R^2-16}\\\\\dfrac{AD^2}{4}+4=R^2\\=AD=2\sqrt{R^2-4}$

По условию AD=2BC.

Значит:

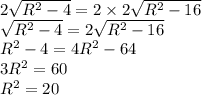
$2\sqrt{R^2-4}=2\times2\sqrt{R^2-16}\\\sqrt{R^2-4}=2\sqrt{R^2-16}\\R^2-4=4R^2-64\\3R^2=60\\R^2=20$

Теперь находим BC и AD:

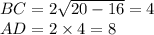
$BC=2\sqrt{20-16}=4\\AD=2\times4=8$

Теперь можно без труда найти площадь трапеции:

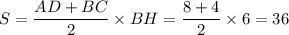
$S=\dfrac{AD+BC}{2}\times BH=\dfrac{8+4}{2}\times6=36$

Получили, что площадь трапеции ABCD равна 36.

Задача решена!

(Для второго случая решить пункт б) невозможно, так как дуга AB + дуга CD по условию должны давать 180°, что невозможно для данного случая)

Zalis1

Геометрия

4,5(48 оценок)

Та, де замість у стоїть 0

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.