urasaya

13.06.2020 06:05

Геометрия

Есть ответ 👍

Осевое сечение конуса – равнобедренный треугольник с углом при вершине 120 и боковой стороной 6 см. Найти объем конуса.Дано и рисунок

234

455

Посмотреть ответы 2

Ответы на вопрос:

Маруся200117

Геометрия

4,4(73 оценок)

Дано:

Конус;

Осевое сечение конуса - равнобедренный △АВС;

∠В = 120°;

АВ = ВС = 6 см.

Найти:

V - ? (см³).

Решение:

Проведём высоту ВН. Получилось два равных прямоугольных треугольника АВН и СВН (их равенство можно также доказать по всем признакам равенства прямоугольных треугольников, исходя из того, что △АВС - равнобедренный).

"Высота, проведённая из вершины равнобедренного треугольника к основанию равнобедренного треугольника, является медианой и биссектрисой".

⇒∠АВН = ∠СВН = 120°/2 = 60°, так как ВН - биссектриса.

СН/СВ = sin ∠CBH ⇒ R = CH = CB ⋅ sin 60˚ = 6 ⋅ √3/2 = 3√3 (см).

Найдём высоту ВН, по теореме Пифагора:

с = √(a² + b²) ⇒ a = √(c² - b²), где a и b - катеты, c - гипотенуза.

a = √(6² - (3√3)²) = √9 = 3 (см).

Итак, ВН = 3 (см).

V = 1/3πR²h = π(1/3 ⋅ (3√3)² ⋅ 3) = 27π (см³).

ответ: 27π (см³).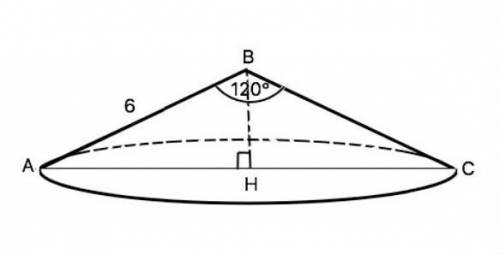
Осевое сечение конуса – равнобедренный треугольник с углом при вершине 120 и боковой стороной 6 см.

tanadzhi01

Геометрия

4,5(92 оценок)

в решении рисунок.

сначала нарисуйте нижнее основание аd. из d восстановите перпендикуляр. нарисуйте угол а, который равен разнице между суммой углов а и в(180°) и углом в.

угол а=180-135=45°.

поскольку угол а=45°, а диагональ вd с основанием аd образует угол 90°,

δ авd равнобедренный прямоугольный.

высота параллелограмма равна основанию аd.

площадь параллелограмма равна произведению его высоты на основание. высота и основание равны, поэтому площадь фигуры можно записать как s=аd²

s=49

аd²=49

аd=√49=7

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.