lizaivleva201

21.03.2021 21:09

Есть ответ 👍

Дана равнобедренная трапеция ABCD. AB – большое основание трапеции и на ней взята точка E так, что угол ∠DEC стал равным углу при основании трапеции. Если DE=6, EC=10, найдите отношение длины отрезка BE к длине отрезка AE. (ответ 9/25)

287

351

Посмотреть ответы 2

Ответы на вопрос:

Angelina13112003

Алгебра

4,7(70 оценок)

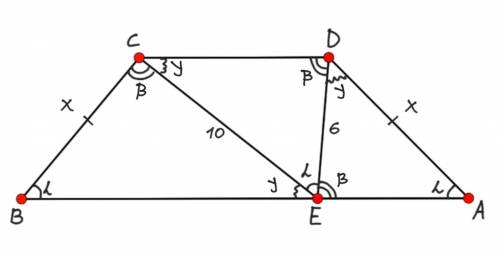
Дано: ABCD — трапеция, ВС=AD, АВ||CD, т.Е∈АВ;

∠СВА=∠DAE=∠DEC, DE=6, EC=10.

Найти: ВЕ:АЕ.

Решение.

∠СВА=∠DAE=∠DEC=α.

∠DEA=∠CDE=β как накрест лежащие при секущей ED и AB||CD.

∠BEC=∠ECD=γ как накрест лежащие при секущей ЕС и AB||CD.

Прямая АВ, т.Е лежит на ней. ∠ВЕС+∠CED+∠DEA=180°.

В ΔCBE: ∠CBA=α, ∠BEC=γ, ∠ВСЕ=β.

В ΔEDC: ∠DEC=α, ∠CDE=β, ∠ECD=γ.

В ΔEAD: ∠DAE=α, ∠DEA=β, ∠EDA=γ.

Треугольники СВЕ, EDC и EAD подобны (по трем углам)

Значит, их соответственные стороны относятся.

Пусть BC=AD=x.

Через подобные треугольники СВЕ и EAD найдем (выразим) стороны ВЕ и АЕ.

1) ВЕ/AD=CE/ED;

BE/x= 10/6;

BE= 10x/6;

BE= 5x/3.

2) BC/AE=CE/ED;

x/AE= 10/6;

AE= 6x/10;

AE= 3x/5.

BE:AE= 5x/3 : 3x/5 = 5x/3 • 5/3x= 25x/9x= 25:9.

ответ: ВЕ:АЕ=25:9.

teenwolfgrrArina

Алгебра

4,5(53 оценок)

Подставим х: у^2-2у-6=9 у^2-2у-15=0 д=4+60=64 у1=(2-8)/2=-3 х1=0 у2=(2+8)/2=5 х2=8

Задай свой вопрос

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.