Регистрация Спросить otvet5GPT
liza0281
30.12.2020 06:21
Геометрия
Есть ответ 👍

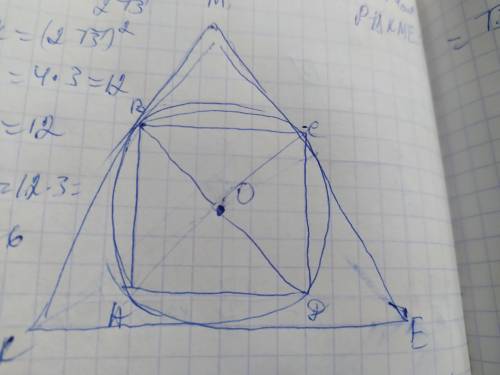
Площа квадрата, вписаного в коло, дорівнює 24 см2. Знайдіть периметр правильного трикутника, описаного навколо даного кола. а)24
б)18
в) 64
г) 32​

293
337
Посмотреть ответы 3

Ответы на вопрос:

Kisson
Kisson
4,6(39 оценок)

ответ: у меня получается ответ 36 см

Объяснение: площадь квадрата =а², где а его сторона, поэтому сторона а=√24

Теперь найдём радиус описанной окружности вокруг квадрата по формуле: R=a√2/2=√24×√2/2=

=√48/2=2√3см

R=2√3см. Поскольку треугольник и квадрат равносторонние, они имеют один и тот же центр окружности, и теперь найдём стороны треугольника, зная радиус окружности, которая вписана в треугольник по формуле: r=a/2√3

a=2√3×r

a=2√3×2√3

a=4×3

a=12

Сторона треугольника=12, тогда его периметр=12×3=36см

Р=36см


Площа квадрата, вписаного в коло, дорівнює 24 см2. Знайдіть периметр правильного трикутника, описано
pinelike
pinelike
4,4(69 оценок)

36 см.

Верного варианта ответа нет.

Объяснение:

1. S квадрата = 1/2d², где d - диагональ квадрата, тогда

1/2d² = 24

d² = 48

d = √48 = 4√3.

2. d = 2R, где R - радиус круга, описанного около квадрата.

4√3 = 2R, тогда R = 2√3.

3. Для треугольника данный круг является вписанным.

По теореме сторона правильного треугольника а = 2r√3, где r - радиус вписанного круга.

В нашем случае r = 2√3, тогда а = 2r√3 = а = 2 · 2√3 · √3 = 12 (см).

Р = 3·а = 3·12 = 36 (см).

FedShar28
FedShar28
4,4(50 оценок)

а зачем ему "нужин" ты?

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Геометрия

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS