elvira125

02.04.2022 06:43

Алгебра

Есть ответ 👍

До ть розв'язати 16.16, будь ласка!!!

277

284

Посмотреть ответы 2

Ответы на вопрос:

NoNameKek1Himka

Алгебра

4,8(82 оценок)

ответ: 3,5

Объяснение:

Решите уравнение lgx·log₂x = lg2 и найдите сумму его корней

Решение

Преобразуем логарифм по основанию 2 в десятичный логарифм применяя свойства логарифма

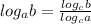
$log_ab=\frac{log_cb}{log_ca}$

Подставляем $log_2x=\frac{lgx}{lg2}$ в исходное уравнение

lgx·log₂x = lg2

$lgx\cdot\frac{lgx}{lg2}=lg2$

Умножим обе части уравнения на lg2

(lgx)² = (lg2)²

(lgx)² - (lg2)² = 0

(lgx - lg2)·(lgx + lg2) = 0

lgx = lg2 lgx = -lg2

x₁ = 2 x₂ = 1/2

Сумма корней уравнения

x₁ + x₂ = 2 + 0,5 = 3,5

Рішення

Перетворимо логарифм по підставі 2 в десятковий логарифм застосовуючи властивості логарифма

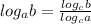
$log_ab=\frac{log_cb}{log_ca}$

Підставляємо $log_2x=\frac{lgx}{lg2}$ в початкове рівняння

lgx·log₂x = lg2

Помножимо обидві частини рівняння на lg2

(lgx)² = (lg2)²

(lgx)² - (lg2)² = 0

(lgx - lg2)·(lgx + lg2) = 0

lgx = lg2 lgx = -lg2

x₁ = 2 x₂ = 1/2

Сума коренів рівняння

x₁ + x₂ = 2 + 0,5 = 3,5

ponomareva1947

Алгебра

4,6(42 оценок)

$\frac{sin^{2}\alpha-3co\alpha s^{2}\alpha}{2sin^{2}\alpha+cos^{2}\alpha} =\frac{\frac{sin^{2}\alpha}{cos^{2}\alpha}-\frac{3cos^{2}\alpha}{cos^{2}\alpha}}{\frac{2sin^{2}\alpha}{cos^{2}\alpha}+\frac{cos^{2}\alpha}{cos^{2}\alpha}}=\frac{tg^{2}\alpha-3}{2tg^{2}\alpha+1}=\frac{5^{2}-3 }{2*5^{2} +1}=\frac{25-3}{50+1}=\frac{22}{51}$

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.