Регистрация Спросить otvet5GPT
9Mesut8
04.05.2023 07:43
Математика
Есть ответ 👍

Егорка задумал четное натуральное число N, и умножил сумму всех его нечетных делителей на сумму всех его четных делителей и прибавил 1. Получился точный квадрат. Докажите, что Егорка ошибся.

263
445
Посмотреть ответы 2

Ответы на вопрос:

kpy4
kpy4
4,7(87 оценок)

Пусть N имеет натуральные делители 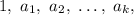1,\ a_1,\ a_2,\ \ldots,\ a_k, и их сумма равна A. Пусть, кроме того, 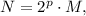N=2^p\cdot M, где N - нечетное число.

Четные делители числа N имеют вид

2,\ 2a_1,2a_2,\ \ldots, 2a_k;\ 2^2,\ 2^2a_1,\ \ldots,\ 2^2a_k;\ldots;\ 2^p,\ 2^pa_1,\ \ldots,\ 2^pa_k.

Складывая четные делители группами в соответствие с тем, сколько множителей вида 2 в них есть, а потом складывая эти группы, получим

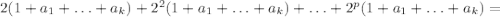
2(1+a_1+\ldots+a_k)+2^2(1+a_1+\ldots+a_k)+\ldots + 2^p(1+a_1+\ldots +a_k)=

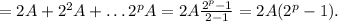
=2A+2^2A+\ldots 2^pA=2A\frac{2^p-1}{2-1}=2A(2^p-1).

Требуется проверить, может ли

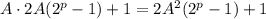
A\cdot2A(2^p-1)+1=2A^2(2^p-1)+1

быть полным квадратом, то есть равняться B².

Конечно, такого быть не может, так как если перенести 1 направо, мы получили бы

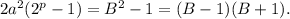
2a^2(2^p-1)=B^2-1=(B-1)(B+1).

Выражение, стоящее слева, делится на 2, но не делится на 4, выражение же, стоящее справа, или является нечетным (если B четное), или же делится не только на 4, а даже на 8 (хотя нам это и не нужно) -- ведь из двух последовательных четных чисел одно обязательно делится на 4.

timoshaisaev
timoshaisaev
4,7(50 оценок)
3,8,15,24,35,48,63,80 . к каждому ответу последовательно прибавляются нечетные числа 3+5=8 8+7=15 15+9=24 24+11=35 35+13=48 48+15=63 63+17=80 2,5,4,7,8,9,16 ,11 , 32, чётные-умножаются на 2,к нечётным-прибавляется 2 2*2=4 5+2=7 4*2=8 7+2=9 8*2=16 9+2=11 16*2=32

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS