Напишите уравнения касательной плоскости и нормали к заданной поверхности в точке (100,)
Ответы на вопрос:
Пошаговое объяснение:
1 Частные производные для F(x,y,z)=1
dFx=2x, dFy=-2y, dFz=-2z
Значения частных производных в заданной точке - это координаты вектора нормали для касательной плоскости N=(2,4,-4)
Уравнение плоскости A*x+B*y+C*z+D=0
A=Nx=2 B=Ny=4 C=Nz=-4
D=-(Nx*Mx+Ny*My+Mz*Mz)=-(2*1+4*(-2)+(-4)*2)=14
Плоскость 2x+4y-4z+14=0
Нормаль (x-1)/2=(y+2)/4=(2-z)/4
2 Частные производные для F(x,y,z)=2
dFx=2xz-2y^3, dFy=-6xy^2, dFz=12z^3+x^2
Значения частных производных в заданной точке - это координаты вектора нормали для касательной плоскости N=(0,-6,13)
Уравнение плоскости A*x+B*y+C*z+D=0
A=Nx=0 B=Ny=-6 C=Nz=13
D=-(Nx*Mx+Ny*My+Mz*Mz)=-(0*1+(-6)*1+13*1)=-7
Плоскость -6y+13z-7=0
Нормаль (1-y)/6=(z-1)/13
3. Производные на вложенном изображении.
Чтобы перейти к целым числам значения производных в т (1,1,1) домножены на 6.
Вектор нормали тогда N=(3,5,38)
Уравнение плоскости 3x+5y+38z-46=0
Нормаль (x-1)/3=(y-1)/5=(z-1)/38
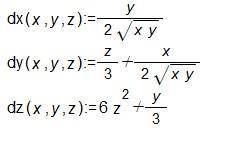
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Математика
-
Производная функции y=in5x при x=1...
 Ekaterina234818.11.2021 10:44
Ekaterina234818.11.2021 10:44 -
Это слово ппроизошло из латинского языка и употребляется в качестве...
 khamraevmowfdcs29.07.2020 12:28
khamraevmowfdcs29.07.2020 12:28 -
На какое расстояние следует отодвинуть от основания саженца клёна...
 VaDerSs25.10.2021 04:52
VaDerSs25.10.2021 04:52 -
Найти производные данных функций. для функции заданной в пункте...
 Artemkizaru29.07.2021 22:42
Artemkizaru29.07.2021 22:42 -
Поезд прошел 60 км и был остановлен на 12 мин. оставшиеся 60 км...
 котик96326.01.2023 03:51
котик96326.01.2023 03:51 -
Первый лыжник за 2 часа проехал 18 км, а второй лыжник за 3 часа...
 Fartyw14.06.2022 23:20
Fartyw14.06.2022 23:20 -
1. реши : вчера температура воздуха была +1°с. за ночь она понизилась...
 girlgood218.02.2020 04:23
girlgood218.02.2020 04:23 -
Поиск результатов по фразе для ремонта квартиры купили 7 рулонов...
 Andreysha36322.11.2020 05:24
Andreysha36322.11.2020 05:24 -
Что можно сделать для улучшения охраны водоемов от загрязнения...
 Hackerywka16.10.2021 12:59
Hackerywka16.10.2021 12:59 -
Дібрати цитати з прикладами турботи, милосердя, самопожертви з твору...
 LizaMelehina45721.12.2021 17:06
LizaMelehina45721.12.2021 17:06

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.
