RomashechkaRomova

05.07.2020 11:12

Геометрия

Есть ответ 👍

С РЕШЕНИЕМ линия пересечения сферы и пооскости имеет длину12 п см Найдите расстояние от центра сферы до этой пооскости если лиаметр равен 16 см (если можно с рисунком)

162

455

Посмотреть ответы 2

Ответы на вопрос:

UlianaTir

Геометрия

4,5(3 оценок)

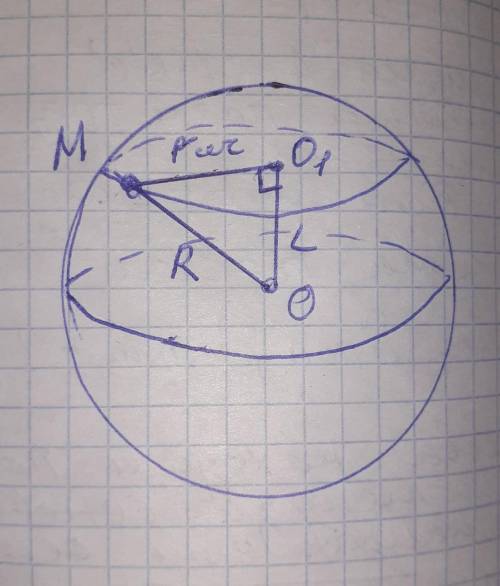
расстояние от центра сферы до плоскости сечения

L=2√7 см

Объяснение:

линия пересечения сферы это длина окружности данного сечения

Ссеч=12π см

диаметр сферы Dc=16см

радиус сферы R=Dc/2=16/2=8см

найти расстояние от центра сферы до плоскости сечения L - ?

расстояние от центра сферы до плоскости сечения , это самое короткое расстояние которое перпендикулярно к плоскости сечения.

и образует прямой угол .

возмем некоторою точку М лежащего на окружности этого сечения, расстояние от точки до центра О1 сечения будет радиусом сечения r.

А от точки М до центра О сферы радиусом сферы R=8см

выходит прямоугольный треугольник Δ ОМО1

где МО=R=8 гипотенуза,

ОО1 = L и МО1=rсеч катеты

находим радиус сечения rсеч=MO1

длина окружности сечения составляет Ссеч=12π см

формула окружности выглядит так

С=πD=2πr отсюда радиус r=С/2π

rсеч=МО1= Ссеч/2π=12π/2π=6 см

расстояние между плоскостью сечения и центром сферы находим по теореме Пифагора

L=OO1=√R²-rcеч²=√МО² - МО1² =

=√8² - 6²=√64-36=√28=√4×7=2√7 см

С РЕШЕНИЕМ линия пересечения сферы и пооскости имеет длину12 п см Найдите расстояние от центра сферы

Anna191203

Геометрия

4,6(64 оценок)

b = 2a · sin α/2 - третья сторона треугольника, лежащего в основании пирамиды

s = 0.5 a · a · sin α = 0.5a²·sinα - площадь основания

проекцией бокового ребра на основание является радиус окружности, описанной вокруг основания

r = a · a · b/(4s) = a · a · 2a · sin α/2 : (4 · 0.5a²·sinα) = а/(2cos α/2)

h = √(a² - r²) = √(a² - a²/(4cos² α/2)) = a √(1 - 1/(4cos² α/2)) - высота пирамиды

объём пирамиды равен v = 1/3 · s · h =

= 1/3 · 0.5a² · sin α · a√(1 - 1/(4cos² α/2)) =

= a³ · 2 sin α/2 · cos α/2 · √(4cos² α/2 - 1) / (6 · 2 cos α/2) =

= a³/6 · sin α/2 · √(4cos² α/2 - 1)

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.