Регистрация Спросить otvet5GPT
максик84
06.06.2023 17:24
Алгебра
Есть ответ 👍

Уравнение (равенство произведения нулю).
Решите уравнение: (7−7sinx) (tgx−√3) = 0 :

213
392
Посмотреть ответы 3

Ответы на вопрос:

missanna00
missanna00
4,8(25 оценок)

(7 - 7sin(x))·(tg(x) - √3) = 0,

1) 7 - 7sin(x) = 0 или 2) tg(x) - √3 = 0,

1) 7 = 7sin(x)

sin(x) = 1

x = (π/2) + 2πm, m∈Z

2) tg(x) = √3,

x = arcsin(√3) + πn, n∈Z,

x = (π/3) + πn.

ответ. x = (π/2) + 2πm, m∈Z или x = (π/3) + πn, n∈Z.

kuzhbapolina20
kuzhbapolina20
4,4(26 оценок)

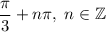
\dfrac{\pi}{3}+n\pi,\;n\in\mathbb{Z}

Объяснение:

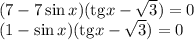
(7-7\sin x) (\mathrm{tg}x-\sqrt{3}) = 0\\(1-\sin x) (\mathrm{tg}x-\sqrt{3}) = 0

ОДЗ:

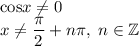
\mathrm{cos}x\ne0\\x\ne\dfrac{\pi}{2}+n\pi,\;n\in\mathbb{Z}

Продолжим решение:

Произведение равно 0, когда хотя бы 1 из его множителей равен 0, а другой при этом не теряет смысла.

Учитывая это, получим:

1)

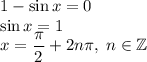
1-\sin x=0\\\sin x = 1\\x=\dfrac{\pi}{2}+2n\pi,\; n\in \mathbb{Z}

Корень не подходит по ОДЗ.

2)

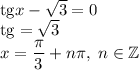
\mathrm{tg}x-\sqrt{3}=0\\\mathrm{tg}=\sqrt{3}\\x=\dfrac{\pi}{3}+n\pi,\;n\in\mathbb{Z}

Этот корень подходит по ОДЗ.

Получаем, что окончательный ответ:

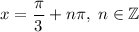
x=\dfrac{\pi}{3}+n\pi,\;n\in\mathbb{Z}

Уравнение решено!

kseniya0090
kseniya0090
4,5(70 оценок)
4x² - 9y² = (2x-3y)(2x+3y), т.к. 2x+3y=4 => 2x-3y=12 x=4, y=4/3 x+3y=8

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS