Lubimka01

20.06.2020 11:05

Геометрия

Есть ответ 👍

Тема 14.
Вектор. Довжина і напрям вектора. Сума векторів та її властивості.
Координати вектора на площині. Скалярний добуток векторів та його
властивості. Проекція вектора на осі координат.
Тема 15.
Система координат на площині. Формула відстані між двома точками
площини. Рівняння прямої і кола.

168

314

Посмотреть ответы 2

Ответы на вопрос:

amino4ka290805

Геометрия

4,6(90 оценок)

Тема 14

Вектор - це напрямлений відрізок, тобто відрізок, який має довжину і певний напрямок. Графічно вектори зображуються у вигляді напрямлених відрізків прямої певної довжини.

Довжина напрямленого відрізка визначає числове значення вектора і називається довжиною вектора або модулем вектора AB.

Для позначення довжини вектора використовують дві вертикальні лінії зліва і справа |AB|.

Вектори, паралельні одній прямій або які лежать на одній прямій називають колінеарними векторами

Два колінеарних вектора a і b називаються Співнаправленими векторами, якщо їх напрямки співпадають: a↑↑b

Додавання векторів (сума векторів) a + b - це операція знаходження вектора c, всі елементи, якого дорівнюють попарній сумі відповідних елементів векторів a і b, тобто кожен елемент вектора c дорівнює:

с = a + b(це вектори додаються)

Властивості:

Формули додавання і віднімання векторів для плоских задач

У випадку плоскої задачі суму та різницю векторів a = {ax ; ay} і b = {bx ; by} можна знайти скориставшись наступними формулами:

a + b = {ax + bx; ay + by}

a - b = {ax - bx; ay - by}

Формули додавання і віднімання векторів для задач

У випадку задачі суму та різницю векторів a = {ax ; ay ; az} і b = {bx ; by ; bz} можна знайти скориставшись наступними формулами:

a + b = {ax + bx; ay + by; az + bz}

a - b = {ax - bx; ay - by; az - bz}

Формули додавання і віднімання n -вимірних векторів

У випадку n -вимірного суму та різницю векторів a = {a1 ; a2 ; ... ; an} і b = {b1 ; b2 ; ... ; bn} можна знайти скориставшись наступними формулами:

a + b = {a1 + b1; a2 + b2; ... ; an + bn}

a - b = {a1 - b1; a2 - b2; ... ; an - bn}

Скалярним добутком двох векторів a і b буде скалярна величина, яка дорівнює добутку модулів цих векторів помноженому на косинус кута між ними:

a · b = |a| · |b| cos α(над векторами ще мають бути рисочки в мене не виходить написати)

Скалярним добутком(інше визначення) двох векторів a і b буде скалярна величина, яка дорівнює сумі попарного добутку відповідних координат векторів a і b.

Властивості скалярного добутку векторів

Скалярний добуток вектора самого на себе завжди більше або дорівнює нулю:

a · a ≥ 0

Скалярний добуток вектора самого на себе дорівнює нулю тоді і тільки тоді, коли вектор дорівнює нульовому вектору:

a · a = 0 <=> a = 0

Скалярний добуток вектора самого на себе дорівнює квадрату його модуля:

a · a = |a|2

Операція скалярного добутку комутативна:

a · b = b · a

Якщо скалярний добуток двох не нульових векторів дорівнює нулю, то ці вектори ортогональні:

a ≠ 0, b ≠ 0, a · b = 0 <=> a ┴ b

(αa) · b = α(a · b)

Операція скалярного добутку дистрибутивна:

(a + b) · c = a · c + b · c

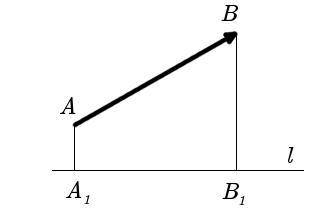
Проекцією вектора AB на вісь l називається число, що дорівнює величині відрізку AlBl вісі l, де точки Al і Bl є проекціями точок A і B на вісь l.

Проекцією вектора a на напрямок вектору b , називається число, яке дорівнює величині проекції вектора a на вісь, що проходить через вектор b.

Малюнок прикріплено)

Тема 15

Система координат б задання точок за до чисел. Кількість чисел, необхідних для однозначного визначення будь-якої точки визначає його вимірність. Ці числа називають координатами. Координати на площині і в тривимірному можна задавати багатьма різними Малюнок прикріплено)

Формула для знаходження відстані між двома точками прикріплена)

Рівняння прямої і кола також прикріплено)

Тема 14. Вектор. Довжина і напрям вектора. Сума векторів та її властивості. Координа

samininav1

Геометрия

4,4(44 оценок)

ты хочеш чтобы мы писали в тетради

Объяснение:

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.