Алгебра: Составить уравнение прямой, не параллельной оси абсцисс, что проходит через точку 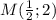и касается графика функции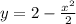 В ответ записать абсциссу точки касания. ответ: 1.

DrNick

08.12.2022 11:38

Алгебра

Есть ответ 👍

Составить уравнение прямой, не параллельной оси абсцисс, что проходит через точку $M(\frac{1}{2};2)$ и касается графика функции $y=2-\frac{x^2}{2}$
В ответ записать абсциссу точки касания. ответ: 1.

205

302

Посмотреть ответы 2

Ответы на вопрос:

mrartemartem1

Алгебра

4,4(58 оценок)

Пусть точка касания равна 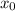x_0 . Составим уравнение касательной к графику функции 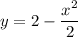$y=2-\dfrac{x^2}{2}$ в этой точке.

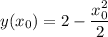
$y(x_0)=2-\dfrac{x_0^2}{2}$

y'=-x

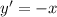
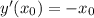
y'(x_0)=-x_0

Уравнение касательной:

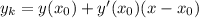
y_k=y(x_0)+y'(x_0)(x-x_0)

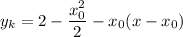
$y_k=2-\dfrac{x_0^2}{2}-x_0(x-x_0)$

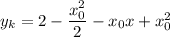
$y_k=2-\dfrac{x_0^2}{2}-x_0x+x_0^2$

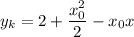
$y_k=2+\dfrac{x_0^2}{2}-x_0x$

Так как касательная проходит через точку 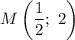$M\left(\dfrac{1}{2} ;\ 2\right)$ , то подставим ее координаты в уравнение:

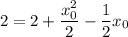
$2=2+\dfrac{x_0^2}{2}-\dfrac{1}{2} x_0$

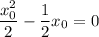
$\dfrac{x_0^2}{2}-\dfrac{1}{2} x_0=0$

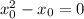
x_0^2-x_0=0

x_0(x_0-1)=0

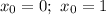
$x_0=0;\ x_0=1$

Проверим получающиеся уравнения касательной. Если 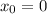x_0=0 :

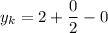
$y_k=2+\dfrac{0}{2}-0$

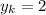y_k=2 - прямая параллельна оси абсцисс - противоречие условию

Если 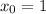x_0=1 :

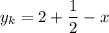
$y_k=2+\dfrac{1}{2}-x$

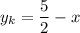$y_k=\dfrac{5}{2}-x$ - корректное уравнение касательной

ответ: 1

Дарина37373

Алгебра

4,4(60 оценок)

Миша-120см маша-240см 1)120-50=70см(опустился) 2) 120+50=170см(маша, когда опустился миша) 3) 170-70=100см=1метр(на 1 метр маша поднимется) ответ: на 1 метр

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.