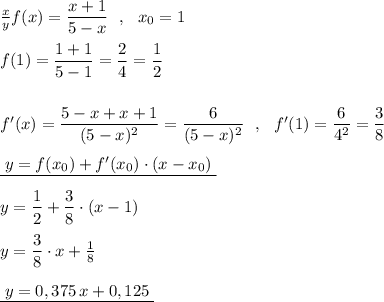Регистрация Спросить otvet5GPT
KINGAsyaKING
05.01.2020 19:15
Алгебра
Есть ответ 👍

Найди уравнение касательной к графику функции f(x)=(x+1)/(5−x) в точке с абсциссой x0=1.

126
404
Посмотреть ответы 3

Ответы на вопрос:

ник5028
ник5028
4,4(46 оценок)

y = 3/8x + 1/8

Объяснение:

Уравнение касательной к графику функции f(x) в точке x0:

y = f(x0) + f'(x0) * (x-x0)

Найдем f'(x), используя формулу: (u/v)' = (u'v - v'u)/(v^2)

u = x+1, u' = 1

v = 5-x, v' = -1

(u/v)' = (5-x + x+1)/(5-x)^2 = 6/(5-x)^2

---

Подставляем значения:

y = 2/4 + 6/16 * (x-1)

y = 0.5 + 3/8*(x-1)

y = 0.5 + 3/8x - 3/8

y = 3/8x + 1/8

kat243
kat243
4,5(27 оценок)

\frac{x}{y} f(x)=\dfrac{x+1}{5-x}\ \ ,\ \ x_0=1\\\\f(1)=\dfrac{1+1}{5-1}=\dfrac{2}{4}=\dfrac{1}{2}\\\\\\f'(x)=\dfrac{5-x+x+1}{(5-x)^2}=\dfrac{6}{(5-x)^2}\ \ ,\ \ f'(1)=\dfrac{6}{4^2}=\dfrac{3}{8}\\\\\underline {\; y=f(x_0)+f'(x_0)\cdot (x-x_0)\; }\\\\y=\dfrac{1}{2}+\dfrac{3}{8}\cdot (x-1)\\\\y=\dfrac{3}{8}\cdot x+\frac{1}{8}\\\\\underline {\; y=0,375\, x+0,125\; }

mickeymouse1958
mickeymouse1958
4,7(65 оценок)

(-бесконечность;+бесконечность)

Объяснение:

(x^2+3)^2=(x^2-3+6)(x^2+3)

(x^2+3)^2-(x^2+3)^=0

x*0=0

x любое число

(3x+2)²-(3x-1)²=12x+6x-1=18x-1 так как x любое число то и выражение (3x+2)²-(3x-1)² имеет область определения (-бесконечность;+бесконечность)

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS