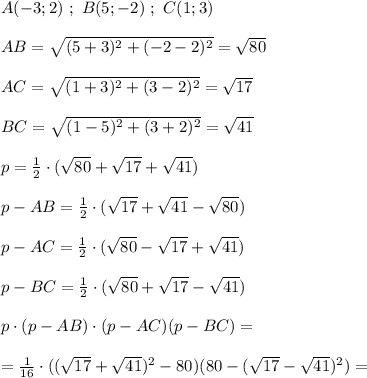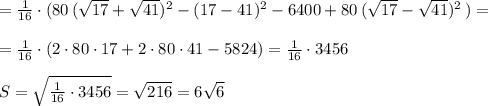Найти площадь треугольника ABC, если A(-3,2), B(5;-2), C(1, 3) - его вершины
277
499
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
с графиком функций! График функции y = kx - 3 1/6 (это дробь)...
 kuraflin66627.03.2020 16:00
kuraflin66627.03.2020 16:00 -
Напишите формулу функции , областью определения которой является...
 pilel23.09.2020 06:50
pilel23.09.2020 06:50 -
напишите формулу функций У=f (x), облостью определения которой...
 ладаседан725.01.2020 17:52
ладаседан725.01.2020 17:52 -
Геометрия ответ жок ...
 serbinaluba66cet29.07.2021 02:02
serbinaluba66cet29.07.2021 02:02 -
Остройте график функции у=2х+3...
 jlenabalkinaoyqk9309.08.2021 02:54
jlenabalkinaoyqk9309.08.2021 02:54 -
Найдите значение выражения 5. 1 _________ 1. 3 – 8.1...
 ruslan563213.09.2020 19:53
ruslan563213.09.2020 19:53 -
с заданием ✍️✍️✍️✍️✍️✍️✍️✍️✍️✍️✍️✍️✍️✍️...
 КУКУ200720.12.2021 16:31
КУКУ200720.12.2021 16:31 -
Вмагазине каль-куль представлены калькуляторы по следующим ценам...
 oksakuvp01cde13.03.2021 07:50
oksakuvp01cde13.03.2021 07:50 -
Втренажерном зале занимаются 6 бухгалтеров, 3 юриста и 6 менеджеров....
 Fulin66623.10.2021 03:24
Fulin66623.10.2021 03:24 -
Найти сумму первых десяти десяти членов арефметической прогрессии...
 хитрыйкот28.01.2021 09:55
хитрыйкот28.01.2021 09:55

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.