Решить систему дифференциальных уравнений двумя Методом исключения неизвестных
2.Методом характеристических уравнений (методом Эйлера)
Ответы на вопрос:
1. Метод исключения неизвестных.
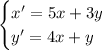
Продифференцируем первое уравнение:
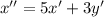
Подставим выражение для y':
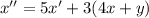
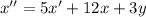
Из получившегося уравнения отнимем первое уравнение системы:
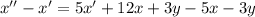
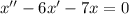
Составим характеристическое уравнение:
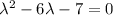
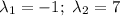
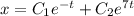
Найдем производную:
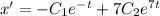
Выразим из первого уравнение системы у:
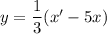
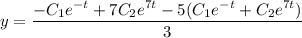
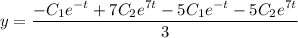
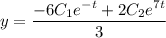
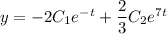
Общее решение:
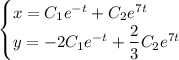
Находим решение задачи Коши:
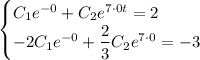
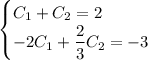
Первое уравнение домножим на 2:
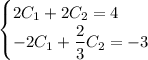
Сложим уравнения:
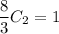
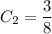
Выразим 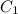 :
:
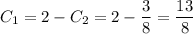
Частное решение:
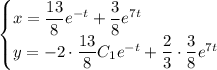
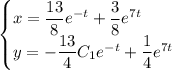
2. Метод характеристических уравнений (метод Эйлера).
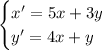
Матрица из коэффициентов при неизвестных:
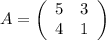
Характеристическая матрица:
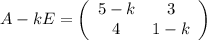
Характеристическое уравнение:
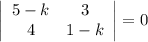
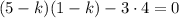
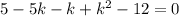
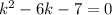
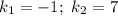
Общее решение:
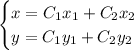
Ищем фундаментальную систему решений:
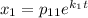
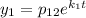
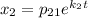
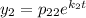
Для нахождения чисел 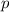 составим систему:
составим систему:
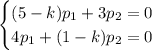
Для 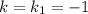 :
:
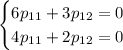
Оба уравнения дают:
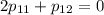
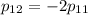
Найдем ненулевое решение. Пусть 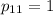 . Тогда
. Тогда 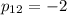 .
.
Для 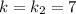 :
:
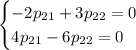
Оба уравнения дают:
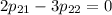
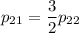
Найдем ненулевое решение. Пусть 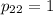 . Тогда
. Тогда 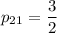 .
.
Фундаментальная система решений найдена:
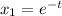
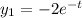
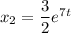
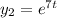
Общее решение:
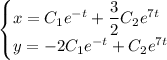
Находим частное решение:
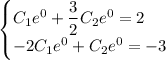
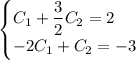
Первое уравнение домножим на 2:
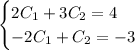
Сложим уравнения:
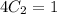
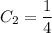
Выразим 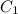 :
:
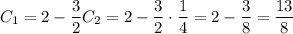
Частное решение:
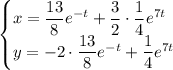
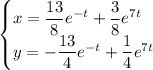
1)460·35% = 460·0,35 = 161 (кг)
ответ. 161 кг картофеля продали в первый день.
пошаговое объяснение:
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Математика
-
Для оформления сцены куплена 120 шаров красных было 5 упаковок по 15 штук сколько...
 Андрей348205.02.2022 08:45
Андрей348205.02.2022 08:45 -
автомобіль за першу годину проїхав 80 км, за. другу на 10% менше ніж ща першу...
 letochka11121.11.2022 11:14
letochka11121.11.2022 11:14 -
Оцінити значення виразу у+3,6×3,5,якщо у=6,8...
 helpmepleasehelp103.08.2021 01:13
helpmepleasehelp103.08.2021 01:13 -
Доведіть нерівність a^2+b^2+4 =ab+2a+2b...
 nunim04.01.2023 00:55
nunim04.01.2023 00:55 -
Две машины из двух городов, которые находятся на расстоянии 816 км друг от друга,...
 yaxyeu27.06.2020 07:35
yaxyeu27.06.2020 07:35 -
Мягкая мебель стоят 15570 руб и Продаётся в кредит 10% первый взнос составляет...
 даша346409.01.2022 19:37
даша346409.01.2022 19:37 -
Найдите объем правильной шестиугольной пирамиды, если ее боковое ребро равно 6,...
 BuMo102.06.2022 05:11
BuMo102.06.2022 05:11 -
Я 5 Кл плз с задачкой : Ленту разрезали на три части Длина первой части равна...
 doda4i27.10.2021 02:06
doda4i27.10.2021 02:06 -
Периметр прямокутника 28 см, одна сторона більша за другу на 2 см. Знайти площу...
 незнайка290115.08.2022 19:04
незнайка290115.08.2022 19:04 -
Во сколько раз объем шара больше объема конуса, высота и радиус которого равны...
 мозг110111.06.2023 17:57
мозг110111.06.2023 17:57

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.
