Найди угловой коэффициент касательной к графику функции f(x)=2x^2+5x+7 в точке с абсциссой x0=2.
ответ:

192

419

Ответы на вопрос:

4,8(65 оценок)

Объяснение:

Угловой коэффициент касательной к графику функции f(x) в точке с абсциссой x0 равен значению производной в этой точке: k = f'(x0).

Находим производную f(x):

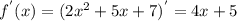
$f^{'}(x) = (2x^{2}+5x+7)^{'}= 4x + 5$

Находим значение производной в точке x0:

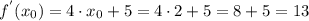
$f^{'}(x_{0}) = 4\cdot x_{0} + 5 = 4\cdot 2 + 5 = 8 + 5 = 13$

4,5(46 оценок)

легко:

(x^10*y^20-1)

всё это верно т.к. мы вынесли за скобку 1

лайк и лучший ответ

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.