ЕВБ

13.07.2022 17:54

Есть ответ 👍

Решите задачу Коши для заданной автономной системы дифференциальных уравнений.

201

473

Посмотреть ответы 2

Ответы на вопрос:

Ekaeterina44

Алгебра

4,6(4 оценок)

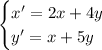
$\begin{cases} x'=2x+4y\\ y'=x+5y\end{cases}$

Продифференцируем первое уравнение:

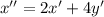
x''=2x'+4y'

Подставим в него соотношение для y' из второго уравнения:

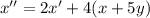
x''=2x'+4(x+5y)

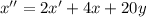
x''=2x'+4x+20y

Из полученного уравнения отнимем первое уравнение системы, умноженное на 5:

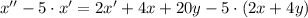
$x''-5\cdot x'=2x'+4x+20y-5\cdot(2x+4y)$

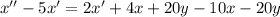
x''-5x'=2x'+4x+20y-10x-20y

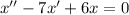
x''-7x'+6x=0

Составим характеристическое уравнение:

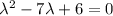
$\lambda^2-7\lambda+6=0$

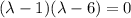
$(\lambda-1)(\lambda-6)=0$

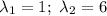
$\lambda_1=1;\ \lambda_2=6$

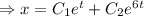
$\Rightarrow x=C_1e^t+C_2e^{6t}$

Найдем х':

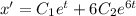
$x'=C_1e^t+6C_2e^{6t}$

Выразим у из первого уравнения:

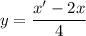
$y=\dfrac{x'-2x}{4}$

Находим у:

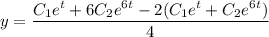
$y=\dfrac{C_1e^t+6C_2e^{6t}-2(C_1e^t+C_2e^{6t})}{4}$

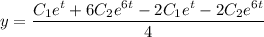
$y=\dfrac{C_1e^t+6C_2e^{6t}-2C_1e^t-2C_2e^{6t}}{4}$

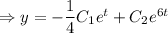
$\Rightarrow y=-\dfrac{1}{4}C_1e^t+C_2e^{6t}$

Условие для задачи Коши:

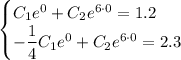
$\begin{cases} C_1e^0+C_2e^{6\cdot0}=1.2 \\ -\dfrac{1}{4}C_1e^0+C_2e^{6\cdot0}=2.3\end{cases}$

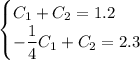
$\begin{cases} C_1+C_2=1.2 \\ -\dfrac{1}{4}C_1+C_2=2.3\end{cases}$

От первого уравнения отнимем второе:

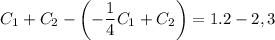
$C_1+C_2-\left(-\dfrac{1}{4}C_1+C_2\right)=1.2-2,3$

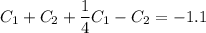
$C_1+C_2+\dfrac{1}{4}C_1-C_2=-1.1$

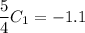
$\dfrac{5}{4}C_1=-1.1$

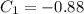
C_1=-0.88

Выражаем из первого уравнения 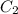C_2 :

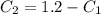
C_2=1.2-C_1

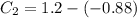
C_2=1.2-(-0.88)

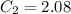
C_2=2.08

Частное решение:

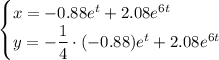
$\begin{cases} x=-0.88e^t+2.08e^{6t} \\ y=-\dfrac{1}{4}\cdot(-0.88)e^t+2.08e^{6t} \end{cases}$

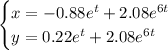
$\begin{cases} x=-0.88e^t+2.08e^{6t} \\ y=0.22e^t+2.08e^{6t} \end{cases}$

hhjufjifklkl

Алгебра

4,6(88 оценок)

Мария - х лет стюарт - у лет маргарет - z лет джек - a лет джордж - b лет x+y+z+a+b=169 x+y=98 y+z=90 z+a=50 a+b=33 (x+y)+(z+a)+b=169 98 + 50 + и = 169, b=21, a=33-21=12 x+90+33=169, x=169-33-90=46, y=98-46=52 z=90-52=38. самый младший в семье джек, ему 12 лет.

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

лорглролрл
15.05.2020 05:01

Решите уравнение: б) (z-4)(2z+1)=0 г) y(3y+7)=0 ж) (1-x)(3x-2)(x+5)=0...
Islami1
10.03.2023 14:41

7класс, тема способы группировки 1. c+d+3x(c+d)=? 2a+ax+2bx+4b=? mn-3m+3-n=?...
Математика666
10.06.2021 04:11

Выражение: а) a³b⁵*a⁴b⁷ б)c⁴d⁷*c⁸d³...
parahonya90
15.04.2023 00:24

Задали на дом эти уравнения, а я в них ни бе ни ме! : ( хотя бы одно!...
Kamelotka
02.11.2022 10:12

Установи соответствие. много...
janeair6994
17.03.2023 00:06

M5-m3+m2-1= Разложите на множители...
ayperi2
05.11.2020 07:06

Упрости выражение и найди его значение при a=5,3. −17a(17a+17)+(17a−17)(17+17a)....
БелинскихАнастасия11
09.08.2021 22:10

решить номера 30 и 31...
B8888
27.04.2023 00:52

Найдите значение выражения X - 2(х+3) при х=7...
milana2709
17.03.2022 14:51

Цилиндр описан около прямой призмы, в основании которой прямоугольный...

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.